Configurations of planet
| Pythagoras of Samos, c. 575-509 BC. Ancient Greek mathematician, founder of the philosophical school. According to his teachings, harmony rules to music, to the movements of celestial bodies, to microworld and to the human soul itself. |
Harmony of spheres
Pythagoras considered his discovery - that sounds whose frequencies are in the ratio of small integers create consonant (euphonious) consonance - to be so fundamental that dared him to generalize to movements in the whole universe. According to Pythagoras, the planets creates harmony - "harmony of the spheres". But we do not hear the sound of this cosmic harmony, because we had been accustomed to it since our birth ...
The first who managed to move the Pythagorean idea a bit further was Johannes Kepler. J.Kepler examined the ratios of distances of the planets from the Sun (he tried to inscrib and circumscribe some regular bodies to spheres of planetary motion) and the ratios of velocities of the planets. He believed that each planetary sphere belongs to one tone of scale.
J.Kepler finally found certain ratios close to integer fractions - ratios of velocities of planets in the perihelion and aphelion. However speeds of planets in the perihelion and aphelion depends on the eccentricity of elliptical orbit of the planet and it changes over time. E.g. Planet Mercury has today eccentricity c. 0.206, but its value may vary about in the limits from 0.121 to 0.232 (and similarly fluctuates also inclination of orbit). It is unlikely that there could be integer ratios between variables that change over time (in the absence of direct dependence of these changes, ...).
Titius’ rule
Titius, Johann Daniel| Titius, Johann Daniel, 1729-1796, German mathematician and physicist. He was interested in theoretical and experimental physics, especially thermometry. |
J.D.Titius replaced (y.1766) Kepler's complicated polyhedra by a simple rule - he expressed the size of the large half-axis (a) as an exponential function of the ordinal number of planet (k):
a ≈ 0.4+0.3*2k [AU]
For k=0,1,2,4,5 Titius formula gives approximate distance for Venus, Earth, Mars, Jupiter and Saturn from the Sun.
After publishing by J.E.Bode (y.1772) in popular astronomy book the rule became known as Bode's Law. After the discovery of Uranus (y.1781) on the orbit corresponding to k=6 the attention of astronomers centered to the orbit k = 3 in the band between Mars and Jupiter, where was (y.1801) discovered asteroid Ceres and later several other smaller bodies - asteroids.
The original Titius' proposal foresaw also a distance of 0.4 AU for Mercury, In this case, however, (as was shown by Charlier) the said series is not geometric, respectively it gives for Mercury k=-∞.
Bode, Johann Elert| Bode, Johann Elert, 1747-1826, German astronomer. Engaged in precision imaging stars and constellations in the map, he issued a stellar atlas and a book on constellations. |
For k=-1,-2,… between Mercury and Venus no body was found and thus for Mercury Titius series fails.
S.F.Dermott (y.1973) showed, that a set of randomly generated periods can be under certain conditions covered by the simmilar rule as the Titius one and questioned so that the planetary orbits are on a logarithmic scale nonrandom.
DecompositionDecomposition into two progressions ... According to the Armellini rule has to be distance of each planet 1.5k: 0.30, 0.45(Mercury), 0.67(Venus), 1.00(Earth), 1.5(Mars), 2.3-3.4(asteroids), 5.1(Jupiter).
Armellini rule covers the planets from Mercury to Jupiter better than the Titius rule.
This rule fails with regard to the prediction of the existence of intramercurial planets series (for k=-3,-4,…), that was not confirmed.
|
Rule |
z |
c1 |
c2 |
k0 |
|
Armellini |
1.5 |
0.0 |
1.0 |
1 |
|
Cameron, Ter-Haaf |
1.69 |
0.0 |
0.225 |
-1 |
|
Blagg, Richardson |
1.728 |
0.0 |
1.0 |
0 |
|
Bélot |
1.883 |
0.28 |
1/214.45 |
-6 |
|
Titius |
2.0 |
0.4 |
0.3 |
1 |
Attempts to approximation generally take the form:
a ≈ c1+ c2 zk – k0 [AU]
For various z, c1, c2 and k0 we get the Armellini, Titius and e.g. also the Bélot's and Cameron's function. Cameron's refines value for Mercury, Bélot's function for Saturn. Only Titius function provides reasonable values up to Uranus.
After the discovery of Neptune (y.1846) and Pluto (y.1930) the ability to analyze distances also between distant bodies arose. J.Iglauer (y.1937) published a series for Saturn, Uranus, Neptune and Pluto for c = 9.99 AU, n = 0,1,2,3 in the form:
a ≈ a(Saturn) + c*n [AU]
and for c1=2.94 c2 =0.27, n=2,3,4,5 in the form:
a ≈ (c1-c2*n)*n² [AU]
Ray Tomes (y.1998) postulated the possibility of existence of standing waves – for outer planets with wavelength (near to twice the Iglauer's constant c) 2*9.8 AU (163 light-minutes) and for inner planets with wavelength 2*0.35 AU (5.8 light-minutes).
According to Charlier Saturn's moons respect the relation: a ≈ 1.5+1.6*1.5k. This relation was modified by A.Mohorovičič to a ≈ 1.0+2.0*1.4k, but it also does not agree with the actual distribution of moons so well, as the Titius relation for the distribution of planets.
According V.Guth and F.Linka are ratios of distances of Saturn moons irregular and these values do not match to the ratios observed for planets. Due to the observed better compliance in moons of Jupiter and Uranus they pronounce a presumption that the system of Saturn's moons does not need to be (with some exceptions: Mimas-Tethys, Enceladus-Dione, ...) yet fully established.
In other theories (e.g. F.Graner, B.Dubrulle, 1994) is Titius rule associated with early development of the Solar systems. Systems of moons could then during the development more sensitive to changes (some moons could be loosed by the planet and others could be obtained from asteroids or comets).
Zenger , Václav Karel
| Zenger , Václav Karel, 1830-1908. Czech mathematician, physicist and astrophysicist, renowned experimenter and inventor. Initiator of the Czech physical terminology. Performed expertise to protect the Eiffel Tower against lightning. |
Back to periods
Original Pythagorean idea did not concern harmony of distances, but rather the harmony of frequencies (and orbital periods).
K.V.Zenger in his treatise on "world electricity" introduced the theory in which he recalculates the orbital periods of the inner planets to Solar (rotation) half-turns (12.6 days).
To preserve the series (with a difference of 11-half-turns) 7 (Mercury), 18 (Venus), 29 (Earth), 40 (?) and 51 (Eros) V.K.Zenger inserted between Earth and orbit of the asteroid Eros a hypothetical planet (with a period c. 500 days)
Approximate periods of Jupiter, Saturn, Uranus and Pluto (12,30,84,248 years) remind powers of numbers 3 (9,27,81,243) increased by 3, Neptune fits into this scheme by the value 2 * 81 + 3 (165 years). There is thus relation:
T ≈ r + s*3k-2 [years]
where r=0 for inner and r=3 for outher planets and s =1 or 2. The pairs (k, s) correspond approximately for (0,2) to Mercury, (1,2) to Venus, (2,1) to Earth, (2,2) to Mars, (4,1) to Jupiter, (5,1) to Saturn, (6,1) to Uranus, (6,2) to Neptune and (7,1) to Pluto. (Extrapolation beyond the known boundaries offers periods (7,2)=486 years, (8,1)=729 years, (8,2)=1458 years, (9,1)=2187 years etc.)
T ≈ 2k/2(2k+2)/6 ≈ 23k/2/6 [years]
From Titius rule for distance comes according to the third Kepler's Law (i.e. after squaring 3/2) approximately relation:
(Extrapolation for k=8 is c. 685 years, for k=9 c. 1935 years).
For systems of satellites was asserted so called Dermott's rule whereby periods of moons are derived as a function of rotation period of the central body.
T ≈ c*T0k [days]
Generalizations
Mary A.Blagg (1913) attempted by calculations based on the relationship
a ≈ c1+ c2 zk [AU]
cover not only the system of the planets but also satellite systems of Jupiter, Saturn and Uranus.
In pursuit of the best possible coverage of known data for value c1 she set a complicated formula (containing goniometric functions,…)
Mohorovičič , Andrija| Mohorovičič , Andrija, 1857-1936, Croatian geophysicist. Dealing with earthquakes, discovered discontinuity velocity of seismic waves. |
A.Mohorovičič (1938) modified the Titius rule to form:
a ≈3.363± 3.363*0.88638k [AU]
with which he tried to describe also some well-known asteroids and comets. Mohorovičić identified some basic conditions which the right relation would have, e.g. it should cover the Sun and stable tracks of asteroids and comets (elements with variable track need not be covered by the relation, ...).
According to Mohorovičič's rule the greatest incidence of bodies is in distance c. 3.363 AU, i.e. in band of asteroids and number of spheres from this point decreases to both sides. Mohorovičič's proposal is quite acceptable for inner system of planets (to which asteroids Eros and Hermes are incorporated before Mars) and for asteroids between Mars and Jupiter. However, for the outer planets spheres with these numbers are formed: 5 (Jupiter) -5 (Saturn) -13 (Uranus) and -17 (Neptune), ...
The result of M.A.Blagg and Mohorovič's efforts is a relatively extensive set of orbits, but it does not cover the whole diversity of the Solar systems.
Quantum mechanicJ.M.Barnothy tried (y. 1947) to modify quantum mechanics so as to be usable even in a macroscopic scale. Based on the assumption that the so called Schrödinger's constant depends on the value of spin, i.e on the rotation of the monitored objects.
In an effort to unify Bohr and Kepler's theory he replaced (y.1973) Schrödinger's constant ћ=h/2π by function ћ ≈ 2s/αk, where s is value of spin and α the constant of fine structure (α ≈ 1/137.0). The fastest spinning planets (Jupiter, Saturn) acquire quantum number k = 2 their neighbors (Uranus, Neptune, Mars, Earth) k = 3 and peripheral body (Mercury, Venus, Pluto) k=4. For the world of atoms is k=0 and for Solar system (as a whole, orbiting a galaxy center) k=6.
He conjectured that the sudden change in the frequency of some pulsars (Crab, Vela) can be explained by jumps from a higher to a lower quantum levels. (I.Velikovskij came with a similar idea, in an attempt to defend its presumption, that Venus came to the Solar Systems just recently.)
G.V.F.MacDonald (y.1963) and F.F.Fish (y.1967) concentrated on relation of the angular momentum and mass of the planet. J.P.Bagby (y.1979) published a comparison of the Titius rule with the Bohr's model of the atom. J.L.Porter continued in these efforts and derived in his wave mechanics quantum numbers from the torque of density μ=ρ a², where ρ=M/r³ (In logarithmic scale he found - depending on the torque of density - two break points in sequence of planetary numbers - one around Mars, the second in the place of Saturn).
Čečelnickij proposed in his theory of so called astrodynamic spectroscopy layering of orbits of the planets, asteroids and moons according to values of effect L=[Ka(1-ε²)]1/2 .
He has defined basic quantum (of spheres kL1,k=1,2,3,…) - for inner planets L1=L(Mercury)/3 = 0.924 km²/s and for outer planets L1=L(Jupiter)/3 = 3.388 km²/s. So he gained space for one more sphere between Saturn and Uranus (c. 13.7 AU, Chiron).
Attempts to exact solution
According V.Guth and F.Linka (y.1947) the regularity of distances of the planets and many months can not be accidental. Distances result from mutual gravitational pull of the central body and the bodies orbiting around it. Internal interplay of gravitational forces acts that -after a certain time- the distance of bodies stabilize to the values describable by some mathematical relationship.
M.W.Ovenden (y.1972) suggested explanation for the Titius rule (Bode law) dynamically - neighboring planets can not be too close. How far should planets be at least may depend on their weights (which would also explain the observed differences of distances between smaller inner planets and larger outer planets).
Music and planet XIn analogy of astronomy and music - more distant planets represents lower tone - whereas our perception of tones is proportional to the logarithm of actual frequencies and also to the logarithm of amplitudes of the actual sound. The closer to each other are tones (on logarithmic scale), the more they hamper to each other. Similarly, it seems to be with the planets (see the Titius' rule) - distant planets must be further apart to each other than planets closer to centre. The deeper tones are also perceived as more powerful - and also outer planets are more massive than interior planets.
Can we expect far from the Sun planet larger than Jupiter???
Arrangement of bodies
The bodies in systems are either equivalent, e.g binaries (such as covalent binding in chemistry, ...) or some of the bodies is stronger (heavier) and determines the behavior of other bodies (ionic binding, ...).
Solar system is system with a strong central body (the Sun) and several slave centers.
Kirkwood Daniel| Kirkwood Daniel, 1814-1889, American mathematician and astronomer, studied the tracks of asteroids and the rotational periods of the planets. Examined in detail some of the gaps in the band of asteroids between Mars and Jupiter. |
The fact that the planet's make up pairs D.Kirkwood (1852) observed among the first.
According to the size, density, distance, rotational periods and distance of the center of gravity from the Sun pairs Jupiter-Saturn and also Uran-Neptune holds together.
According to the distance of the center of gravity (in pair with the Sun) and the size (or density) also Venus-Earth and Mercury-Mars forms pairs; only the rotational period and distance from the Sun tend to prefer rather pairing Mercury-Venus and Earth-Mars.
Orbits of pairs of planets whose rotation periods are approximately identical (Earth-Mars, Jupiter-Saturn, Uranus-Neptune) are in reality closer than predicted by Titius rule.
Types of arangement
According to the position of the smaller body relative to the larger (and central) body we distinguish two types of arrangements:
The lightest inside
Central - Smaller - Bigger
+----+
| | +---+
| | +-+ | |
+----+ +-+ +---+
· the Sun - Mercury - Venus - Earth - Jupiter
· Jupiter - Io - Europa - Ganymed
· Saturn - Mimas - Enceladus - Tethys - Dione - Rhea - Titan
· Uran - Miranda - Ariel - Titan
· Earth – artificial satellites -Moon
Central - Bigger - Smaller
+----+
| | +---+
| | | | +-+
+----+ +---+ +-+
· the Sun - Jupiter- Saturn - Neptune - Pluto
· Jupiter - Ganymed- Kallisto
· Saturn - Titan - Japetus
· Uranus - Titania - Oberon
· Mars - Phobos - Deimos
Exceptions to these schemes are:
- bodies on the same track, e.g. Sun-Trojans/Jupiter, Saturn-Helene/Dione
- bodies about the same size, e.g. Sun-Venus/Earth
Bodies according to influence
Depending on the distance from its center and the distance from the center of the superior system the following cases are distinguished:
- Bodies close to the center (Mars: Phobos, Deimos, Jupiter: the nearest moons)
- Bodies interfered with by other bodies (Laplace's resonance,…)
- Bodies systems disturbed by the center (distant moons of the Jupiter,…)
Symmetry of motion
Motion of geometrical axes
Geometrical axis
Let us consider motion of two bodies P,Q around center S and
motion of thought (undirected, geometrical) axis A of
angle PSQ. At time of planetary conjunction P-Q,
axis A is aligned with line SP =SQ.
During time t the first line cover (with regard
to the original line) angle t/P (*360°), meanwhile the second line
angle t/Q (*360°).
The axis A cover (during time t) angle:
t/Q+(t/P-t/Q)/2 = t/Q+t/(2P)-t/(2Q) = t *(1/(2P)+1/(2Q)) (*360°).
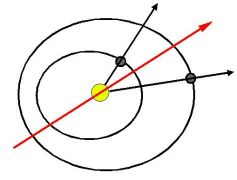 Axial period of two bodies
Axial period of two bodies
Axial period is period, after which the axis of angle P-S-Q align with its original position. Axial period of two orbital periods P, Q is period:
[P,Q] = 2/(1/P+1/Q)= 2∙P∙Q/(Q+P)
We designate axial period with brackets [].
During time [P,Q] axis runs through full angle 360°.
For any periods A,B,C and constant k it holds:
[A,B] = [B,A] [A,A] = A ([A,B],[B,C]) = 2∙(A,C) [k∙A,k∙B] = k∙[A,B]Considering pair of planets P,Q and the Sun, center of mass is always somewhere inside the triangle SunPQ. If we neglect differences in masses and in actions, we can assume, center of mass move in step with axis of angle PsunQ, i.e. with period [P,Q].
We can imagine axial period (in contrast to synodic period)
as an orbital period; (and we can, as the case may be, compare it
with other orbital periods).
Gravity centre of (three) bodies moves (around S) approximately with axial period.
Axial period of more bodies
Axial period of n bodies having periods P,Q,R,S... is determined by harmonic average of given periods:
[P,Q,R,S,...] = n/(1/P+1/Q+1/R+1/S...)
Pair axial periods|
Outer planets |
Inner planets |
[J,S]= 16.91324 years ( 6177.56 days)
[J,U]= 20.78898 years ( 7593.18 days)
[J,N]= 22.13075 years ( 8083.26 days)
[S,U]= 43.62101 years (15932.57 days)
[S,N]= 49.97918 years (18254.89 days)
[U,N]=111.29089 years (40649.00 days)
|
[M,V]=0.346170 years (126.4385 days)
[M,E]=0.388199 years (141.7896 days)
[M,R]=0.427013 years (155.9666 days)
[V,E]=0.761766 years (278.2351 days)
[V,R]=0.927141 years (338.6381 days)
[E,R]=1.305775 years (476.9343 days)
|
Symmetrical configurations
Configuration of more bodies is axially symmetric, when certain axes are identified into one axis. In case of even number of bodies such situation occurs, when all axes of selected pairs of bodies align. Alignment of two axes can be at angle 0° or 180°, so period of alignment is half of synodic period computed from periods of these axes.
Outer planets
Four outer planet of solar system take symmetric configuration with periods:
- ([J,S],[U,N])/2 = (16.9132418,111.2908942)/2 = 19.94423/2 years = 9.97212 years
- ([J,U],[S,N])/2 = (20.7889842, 49.9791756)/2 = 35.59471/2 years = 17.79735 years
- ([J,N],[S,U])/2 = (22.1307494, 43.6210092)/2 = 44.92108/2 years = 22.46054 years
Date (Interval) Math.date
-------------------------------------
2014 Jun 10 AD ( 9.69) 2014.45 JS-UN
2024 Aug 30 AD (10.22) 2024.67
2034 Jul 20 AD ( 9.89) 2034.56
2044 Aug 31 AD (10.12) 2044.67
-------------------------------------
2018 May 6 AD (18.56) 2018.35 JU-SN
2036 Feb 23 AD (17.80) 2036.15
-------------------------------------
2023 May 29 AD (22.08) 2023.41 JN-SU
2046 Jul 13 AD (23.12) 2046.54
Mayan period tzolkin (z) in symmetric configurations (as quantum):
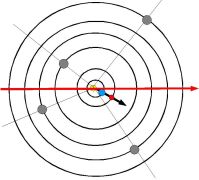
|
Symmetric configurations |
Mayan period (multiple of tzolkin) |
Note |
|
([J,S],[U,N]) = 19.944 years= 7284.6 days |
7280 days = 28*z= 20*364 days = 260*28 days (260 natural months) 7280 days = 21*346.67 days (c. 21 ecliptic years) |
(J,S)= 7253.5 days = 19.86 years |
|
([J,U],[S,N]) = 35.594 years = 13001 days |
13000 days =50*z= 35.59 years 12997.8 days =3*J = 35.59 years |
(S,N)= 13101.5 days = 35.87 years. |
Motion of axes of inner planets measured with regard to axes [J,S] results in periods (n² multiples of quantum q=16.2 days):
([M,V], [J,S]) = ( 63.219, 3089.0) = 64.540 d (2²*q) ([V,E], [J,S]) = (139.118, 3089.0) =145.679 d (3²*q) ([E,R], [J,S]) = (238.470, 3089.0) = 258.420 d (4²*q) ~ tzolkin.Period (V,E)= 583.92 d (6²*q).
Inverse motion
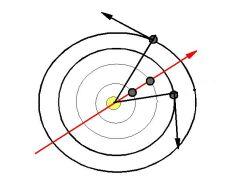
Periodical symmetry
Let us have line r moving with period R around centre. With
regard to line r bodies P and Q move inversely if r is oriented
axis of motion of these two bodies, i.e. when R=[P,Q].
Bodies open and then close angle with regard to r with synodic period (P,Q).
Let us assume, it is not necessary that this motion run continuously. Let the condition of inverse holds at every instant t = k*T, where k is whole number and T time interval (period). At every instant t it holds:
Lp - Lr = Lr - Lq
where Lp,Lq and Lr are longitudes of bodies P,Q and Lr is longitude of line r.
So
frac(T/P)-frac(T/R) = frac(T/R)-frac(T/Q), i.e. 2*frac(T/R) = frac(T/P)+frac(T/Q)
Planets Uranus and Neptune exert approximate inverse motion with regard to places of conjunctions of Jupiter and Saturn.
During time t = (J,S) = 19.859 years positions of outer
planets change in average by angles:
Planet Longitude
Jupiter LJ= frac((J,S)/J)*360° = 242.7°
Saturn LS= frac((J,S)/S)*360° = 242.7°
Uranus LU= frac((J,S)/U)*360° = 85.1°
Neptune LN= frac((J,S)/N)*360° = 43.4°
Differences of longitudes are:
LJ - LU = 242.7*360°-85.1*360° = +157.6°
LN - LJ = 43.4*360°-242.7*360° = -199.3*360° = +160.7°
Deviation is c. 160.7*360°-157.6*360° = 3.1°. Angle 3.1° during 19.859 years corresponds to 360° during c. 2320 years.
Inverse motion U and N with regard to (J,S) is modulated by period H, H is c. 2320 years.
Axial periods of outer planets: [J,S,U] = 23.04990 years, [J,S,N] = 24.13135 years, [J,U,N] = 29.33301 years, [S,U,N] = 57.78284 years
[J,S,U,N] = 29.36395 years. Axes [J,U,N] and [J,S,U,N] move with periods close to Saturn period, periods [S,U,N] is approximately twice of these periods. It applies: [J,U,N] = [S,3H], [J,S,U,N] = [S,4H], see stable resonance/Period H..
Barycentric periods
Two bodies (binary stars) orbit around a common center of gravity
with the same periods.
In the case of more bodies the situation complicates.
Center of gravity is -during motion of two planets around the Sun
(neglecting the difference in mass of the planets)-
always on the geometrical axis of links of planets with the centre - see axial period.
But it (the center of gravity) is moving with axial period
only close to the conjunctions of planets.
During oppositions - "singularities" occurs. At the moment of singularity -physically- nothing special happens - orientation of axis overshoots. So motion of centroid axes recalls rather the wave behavior of atoms, than a simple cyclical motion with a fixed period.
Irregular motion of real axes
Angular velocity of motion of the center of gravity varies, movement of real oriented centroid axes is irregular.
At the moment of opposition the "polarity reversal", i.e. a sudden change in direction of the axis, appears. Centroid axis movement slows and then changes the direction from the central body to the center of gravity by 180º. These "singularities" make it difficult to calculate mean periods of oriented axes motion.
Computation of "instant periods" in conjunctions
dx = dx1m1+dx2m2 /
(m1+m2),
where dxi =
ai cos dϕi, dyi = ai
sin dϕi, dϕi = dt/Pi
E.g. for Jupiter (J) and Saturn (S), dt=1 year (after conjunction J-S),
aJ=5.202 AU, aS = 9.535 AU.
dϕJ = dt/PJ = 30.35°
dxJ = 5.202 * cos(30.35°) = 4.489 AU dyJ =
5.202 * sin(30.35°) = 2.628 AU
dϕS = dt/PS = 12.22°
dxS = 9.535 * cos(12.22°) = 9.319 AU dyS
= 9.535 * sin(12.22°) = 2.018 AU
Σ mi dxi = 317.83*dxJ + 95.16*dxS = 317.83*4.489
+ 95.16*9.319 = 2313.5 [Mearth*AU]
dxi = 5.60 AU
Σ mi dyi = 317.83*dyJ
+ 95.16*dyS = 317.83*2.628 + 95.16*2.018 =
1027.3 [Mearth*AU]
dyi = 2.49 AU
tg(dϕ) = dyi / dxi = 2.49 / 5.60 = 0.4446
dϕ = 23.94°
PJS = 1 rok * 360°/23.94° = 15.03 years
Comparison of paired axial periods
Comparing of pair axial periods with instant pair periods in conjunctions:
|
Periods of undirected geometrical axes |
"Instant periods" computed at conjunctions |
[J,S]= 16.91 years
[J,U]= 20.79 years
[J,N]= 22.13 years [J,S,U,N]= 29.36 years
[S,U]= 43.62 years
[S,N]= 49.98 years
[U,N]=111.29 years
|
[J,S]= 15.03 years
[J,U]= 13.49 years
[J,N]= 15.16 years [J,S,U,N]= 19.03 years
[S,U]= 34.73 years
[S,N]= 41.94 years
[U,N]=123.27 years
|
Mean period of centroid axis computed at time when bodies are on one half-line (i.e. in conjunction) differ from mean periods computed in other starting positions. From elementary angular shifts we obtain e.g. period c. 15 years in conjunction J-S and c. 14 years in quartile J-S.
The real axial period is determined by the heavier of bodies. At the moment of the opposition of bodies centroid axis is directed to the heavier body. Even in the time of conjunction the centroid axis passes the body. Thus, the real centroid axis copies - although by an uneven movement - motion of the heavier of the two planets.
Minimum interaction
Bodies moving in systems maintained by gravitational attraction, paradoxically manifest a kind of "repulsion". Systems prevents accumulation of mass in one place. During extended interaction system passes through a certain evolution. In the end bodies get synchronized and take a certain optimum and stable configuration. This configuration can - in the case of intersecting orbits - exclude collision of bodies (e.g. the motion of the planets Neptune and Pluto).
Analytical mechanicBesides Newtonian mechanics working with vector quantities that have both magnitude and also direction, Leibniz's analytical mechanics was originated at the same time. Analytical mechanics works exclusively with scalar quantities (values of energy ...), so it could therefore be gradually set aside as a purely mathematical science.
Repulsion of bodies
Gravitational attraction of bodies has one quite bit paradoxical consequence.
Bodies on orbits (around central body) repulse each other.
This phenomenon results from principle of conservation
of angular momentum (Alfven).
Electrons on orbits also repulse each other. They have the same charge...
When smaller body moves close to greater body (or more
bodies), it is forced to adapt to repulsion forces.
According to circumstances one of these possibilities takes place:
Smaller body tries:
- move the same way as greater body (trivial resonance)
- synchronize its motion with other bodies (synchronizing resonance)
- to change ellipse of orbit (resonance of eccentricity)
- to change inclination of orbit (resonance of inclination)
- to change direction of motion (backward motion)
If no possibility succeeds, body leaves its orbit (is thrown away) or comes to pieces (is disrupted).
Principle of minimum interaction
After long interaction, bodies form an optimal
configuration and move such a way, that certain summary
characteristic has extreme.
(According to A.M.Molchanov such synchronization would appear
even from action of very week forces.)
For some subsystems of solar system (Io-Europa-Ganymed, satellites of Uranus) Ovenden principle (i.e. variational principle of celestial mechanics) was proved. [Ovenden,1974]. Ovenden principle fails for outer planets.
Ovenden,1974: Ovenden, M.W., Feagin, T., and Graf, O., "On the principle of Least Interaction Action and the Laplacean Satellites of Jupiter and Uranus," Celestial Mechanics Journal, 8(4), 455-471 (1974).
The idea of the principle of minimal interaction:
1/ arbitrarily scattered bodies (understood bodies on random orbits) are synchronized (they regulate phase shifts on tracks mutually), so to have (in long-term scale) the sum of their interactions - which are a function of their real (or angular) distance and weight - minimal.
2/ originally random orbits are modified (while keeping the total energy of system ..), in order to further minimize the total interaction (and new orbits again readjust their phase shifts by 1/)
By 1/ so Galilean moons act
By 2/ e.g. position of Venus and Earth between the Sun and Jupiter had to be gradually adjusted so that some characteristics become balanced?!
IllustrationThe cases are divided according to ratio of synodic periods relative to one (outer) "fixed" body.
Three bodies
Cases are partitioned according to ratios of synodical periods with regard to a given (outer) "fixed" body.
Three bodies:
Case 2:1
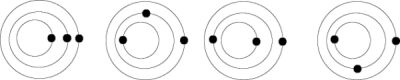
Case 3:1
(Io-Europa-Ganymed, Miranda-Ariel-Umbriel)
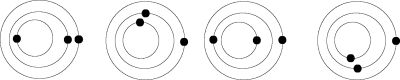
Case 3:2
(5:2, 7:2, 9:2,...)
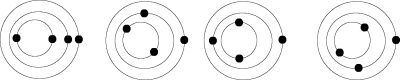
Case 4:3
(8:3,16:3,...)
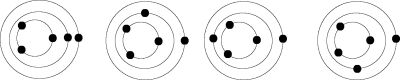
Case 5:4
(7:4, 9:4, ...)
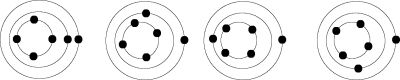
Planets in distance
18.8.2003 Noteworthy configuration
Noteworthy configuration
Regarding minimal interaction - configuration of planets in the period 18.8.2003-31.8.2003 is interesting.
Let us mark V-Venus, E-Earth, R-Mars, J-Jupiter, U-Uran and observe heliocentric conjunctions and oppositions.
18.8.2003 opposition V-E, 21.8.2003 conjunction V-J, 22.8.2003 opposition E-J 24.8.2003 conjunction E-U 27.8.2003 R nearest to E, Moon in Nov, 28.8.2003 conjunction R-E 30.8.2003 R in perihelion, 31.8.2003 Moon in perihelion.It seams like distances: J-U, J-E, J-R, E-V, R-V, (U-V), R-Moon maximized in this configuration.
In the moment of nearest approach of Mars to Earth, the adjacent (concurrent) bodies Jupiter and Venus are found on the opposite site of the Solar system.
In the following text we proceed from oppositions J-U, in the year 2003 the exact opposition J-U come till 31.10.2003.
Similar configurations
We find some other similar configurations in years 719.29, 1147.48, 1575.66, i.e. with approximately Babylonian period with regard to 2003.84: 31*(J,U) = 31*13.8123 years =428.18 years.
Period 12J
719 - 862 - 1004,
1147 - 1290 - 1433,
1575 - 1718 - 1861,


