The Last Fermat theorem - F-sums in sequences
Now take a more general problem. Let us search all (arithmetic) sequences f= {f(i)} that have such members f(r),f(b),f(c), which satisfy so called F-sum: f(r)+f(b)=f(c).
Fermat’s theorem reduces field of sequences to f(n) = nk (k is constant), which means that F-sums ak +bk =ck are observed.
Basic terms
Arithmetical sequences
Sequence {f(t)} is called arithmetical sequence of k-th order, if its k-th differential sequence is constant.
Arithmetical sequences are results of algebraic functions
with constant exponents (linear and power functions,...).
If {d(t)} is differential sequence of sequence {f(t)}, then {f(t)}
is sum sequence of sequence {d(t)}.
Characteristics
Let us call characteristic of sequences the set of first numbers of particular differential sequences (starting with constant sequences).
Any sequence with given leading element has just one characteristic.
E.g. sequence or third powers is of third order with characteristic [6,6,1,0]:
0, 1, 8, 27, 64, 125, 216, 343, 512, 729, ...
1, 7, 19, 37, 61, 91, 127, 169, 217, ...
6, 12, 18, 24, 30, 36, 42, 48, ...
6, 6, 6, 6, 6, 6, 6, 6, ...
We write characteristic from below, i.e. beginning with constant sequences. But, to simplify some next formulas, let us index it from above.
Elements of characteristics {r(h))} are then... r2,r1,r0; in our example [6,6,1,0] is r0=0,r1=1,r2=6,r3=6.
Sequence D, that results from sum (differences) of characteristic RD= RA + RB of sequences A and B, is equal to sum of these sequences, i.e. D=A+B.
Sum of characteristics of sequences of different orders have to
be done from the right with missing left position completed by zeros.
E.g. the sum of characteristic [6,6,1,0] of sequence A=f(t) = t³ and [2,1,0] of sequence B=g(t) = t²
is characteristic RD= [6,8,2,0] of sequence D=f(t)+g(t)=t³+t²:
Charakter. Sequence
─────────────────────────────────────────────
RA= [6,6,1,0] A= {0,1, 8,27,64,125,216,... }
RB= [0,2,1,0] B= {0,1, 4, 9,16, 25, 36,... }
─────────────────────────────────────────────
RD= [6,8,2,0] D= {0,2,12,36,80,150,252,... }
Elementary sequences
Zero sequence, i.e. sequence {0,0,0,0,0,...} has all differential sequences filled by zero. Therefore it can represent all sequences of any order, i.e.sequences with characteristics [0],[0,0],[0,0,0], and so on.
We call basic sequence of order k the sequence s with characteristic of the form: [1,0,0...,0,r(0)], i.e. with constant 1 of the last difference sequence (i.e. r(k)=1) and with zero shift of the next differential sequences (i.e. for h ε <1,k−1> is r(h)=0). Individual basic sequences are distinguished by the number r(0).
Characteristics of basic sequences
for k=0..5:
• k=0: [1]
• k=1: [1,r0]
• k=2: [1,0,r0]
• k=3: [1,0,0,r0]
• k=4: [1,0,0,0,r0]
• k=5: [1,0,0,0,0,r0]
For each F-sum (a, b, c) a basic sequence [1,0, ... 0, rk] can be created from zero sequence. The zero sequence reflects an infinite number of elementary sequences.
The basic sequences are easy to read and assemble. But they are not in its entirety growing - their first two members are the same. That is why we are now introducing another type of sequences ... The starting sequence of order k is called a sequence with a characteristic of the form: [1,1,1 ..., 1, r(0)].
Characteristics of starting sequences
for k=0..5:
• k=0: [1]
• k=1: [1,r0]
• k=2: [1,1,r0]
• k=3: [1,1,1,r0]
• k=4: [1,1,1,1,r0]
• k=5: [1,1,1,1,1,r0]
Interchangeable sequences
Sequences are called interchangeable, if they are identical, except indexes of their members. E.g. sequences with characteristics [6,6,1,0] and [6,0,1,−1] are equivalent.
Charakter. Sequence
─────────────────────────────────────────────
[6,6,1,0] { 0,1,8,27,64,125,216,... }
[6,0,1,−1] {−1,0,1, 8,27, 64,125,216,.}
More generally – (in this example for m=0, resp.−1) all sequences [6,6(m+1),3m²+3m+1, m³] are interchangeable.
F-sequences
If there exists numbers f(a),f(b),f(c) in sequence {f(n)} = f(0),f(1),f(2),... such, that it holds f(a)+f(b)=f(c), we speak of F-sum.
F-sum is identified by F-indexes (a,b,c), 1≤ a < b < c.
In the following table sequences with characteristics [6,6,1,0..8] are written, together with their first existing F-sum (in first 100 members of sequences) and its F-indexes.
Charakter. Sequence F-indexes F-sum
──────────────────────────────────────────────────────────
[6,6,1,0] {0,1,8,27,64,125,… }
[6,6,1,1] {1,2,9,28,65,126,… } ( 6, 8, 9) 217+513=730
[6,6,1,2] {2,3,10,29,66,127,…} ( 5, 6, 7) 127+218=345
[6,6,1,3] {3,4,11,30,67,128,…}
[6,6,1,4] {4,5,12,31,68,129,…}
[6,6,1,5] {5,6,13,32,69,130,…}
[6,6,1,6] {6,7,14,33,70,131,…} (43,58,65) 79513+…=274631
[6,6,1,7] {7,8,15,34,71,132,…} ( 0, 1, 2) 7+8=15
[6,6,1,8] {8,9,16,35,72,133,…} (12,16,18) 1736+4104=5840
E.g. in sequence {7,8,15,34,71,132,223,...} is third member (15) sum of previous two members (7+8).
We call F-sequences the sequences that have F-sum.
Multiples of sequences
Let sequence f'(n) is q multiple of sequence f(n), i.e. f'(n)=q∙f(n).
Characteristic R' of sequence f'(n) is q multiple of characteristics R, i.e. r'(m)=q∙r(m), mεN, qεN.
If there exists F-sum with indexes (a,b,c) in sequence f(n), then there exists analogous F-sum (with the same indexes) in sequence f'(n).
E.g. F-sum with indexes (0,2,5) exists in all sequences with characteristics [1,0,9], [2,0,18], [3,0,27], [4,0,36],...
Charakter. Sequence F-indexes F-sum
───────────────────────────────────────────────────────────
[1,0,9] {9,9,10,12,15,19,24,...} ( 0, 2, 5) 9+10=19
[2,0,18] {18,18,20,24,30,38,48,.} ( 0, 2, 5) 18+20=38
[3,0,27] {27,27,30,36,45,57,72,.} ( 0, 2, 5) 27+30=57
[4,0,36] {36,36,40,48,60,76,96,.} ( 0, 2, 5) 36+40=76
If sequence f(n) is F-sequence, then all sequences a'(n) are also F-sequences, for qεN.
Sequences having equal F-indexes
To given F-indexes (a,b,c) entire class of sequences (subset of all sequences) exists with necessary F-sums.
In other words: for each F-sum of a given sequence there exists always an analogous F-sum also in others sequences.
It shows that:
- Zero sequence contains all possible F-sums.
- There exists sequences, that contains infinite number of F-sums (e.g. sequence f(n) = n²).
- There exists sequences, that have no F-sum (e.g. sequence f(n) = n³).
- Two given F-sums can exist also in more sequences. Thus we may not always get two different sequences from the transformation of two different F-sums from one sequence.
E.g. F-sums with indexes (6,8,10) and (5,12,13) exist in both the sequences: with characteristics [2,1,0] and [1,0,2].
Charakter. Sequence
─────────────────────────────────────────────────────────
[2,1,0] {0,1,4,9,16,25,36,49,64,81,100,121,144,169..}
[1,0,2] {2,2,3,5, 8,12,17,23,30,38, 47, 57, 68, 80..}
In [2,1,0] is 36+64 = 100 and in [1,0,2] is for the same indexes 17+30=47. Similarly is 25+144 = 169 and 12+68=80.
- To given F-sum there exists one equivalent in zero sequences and one equivalent in certain basic sequence.
- Two sequences have F-sums with the same indexes (a,b,c), if it holds for characteristics r(m) and r'(m):
∑Δr(m)∙( 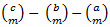 ) = 0; (m=0..k) ) = 0; (m=0..k)
|
where Δr(m) = r'(m)−r(m) and
![]() ,
,
![]() ,
,
![]() are binomial coefficients.
are binomial coefficients.
Because 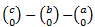 ) = 1−1−1 = −1,
we can evaluate r(0) from the previous formula:
) = 1−1−1 = −1,
we can evaluate r(0) from the previous formula:
∑Δr(0)= ∑Δr(m)∙(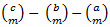 );
(m=1..k) );
(m=1..k)
|
For m=1 it holds Δc(0)=Δc(1)∙(c−b−a). For (0,2,5) is c−b−a= 5−2−0=3.
So F-sum with indexes (0,2,5) exists also in sequences [1,1,12],[1,2,15],..., [2,1,21],[2,1,24], and so on.
Charakter. Sequence F-indexes F-sum
──────────────────────────────────────────────────────────
[1,1,12] {12,13,15,18,22,27,33,..} ( 0, 2, 5) 12+15=27
[1,2,15] {15,17,20,24,29,35,42,..} ( 0, 2, 5) 15+20=35
[1,3,18] {18,21,25,30,36,43,51,..} ( 0, 2, 5) 18+25=43
[1,4,21] {21,25,30,36,43,51,60,..} ( 0, 2, 5) 21+30=51
────
[2,1,21] {21,22,25,30,37,46,57,..} ( 0, 2, 5) 21+25=46
[2,2,24] {24,26,30,36,44,54,66,..} ( 0, 2, 5) 24+30=54
[2,3,27] {27,30,35,42,51,62,75,..} ( 0, 2, 5) 27+35=62
─────
[3,1,30] {30,31,35,42,52,65,81,..} ( 0, 2, 5) 30+35=65
[3,2,33] {33,35,40,48,59,73,90,..} ( 0, 2, 5) 33+40=73
Let us try to deduce (according to previous rules) basic sequences, that have F-sums analogous to selected Pythagorean F-sums, i.e. F-sums (3,4,5), (6,8,10) and (5,12,13), from power sequences of 2.order.
Let us look for such r0, that respect relation of transformation from sequence with characteristic Rm=[2,1,0] to sequences with characteristic Rz=[1,0,r0].
Difference of these two characteristics is ΔR=[1,0,r0]−[2,1,0]=[−1,−1,r0].
It holds:
Δr0=Δr2∙(
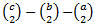 )+Δr1∙(
)+Δr1∙(
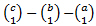 ).
).
After substitution we get for a=3,b=4,c=5: Δr0=+1,
for a=6,b=8,c=10:Δr0=+2
and for a=5,b=12,c=13 also: Δr0=+2.
Therefore basic sequence for F-sum with indexes (3,4,5) is:
[1,0,1] and for F-sums with indexes (6,8,10) and (5,12,13): [1,0,2].
Charakter. Sequence F-sum
──────────────────────────────────────────────────────────
[2,1,0] {0,1,4,9,16,25,36,49,64,81,100,121,…} 9+16= 25
[1,0,1] {1,1,2,4,7,11,16,22,29,37,46,56,67,…} 4+7= 11
───────────────────────────────────────────────────────────
[2,1,0] {0,1,4,9,16,25,36,49,64,81,100,121,…} 36+64=100
[1,0,2] {2,2,3,5,8,12,17,23,30,38, 47, 57,… } 17+30= 47
───────────────────────────────────────────────────────────
[2,1,0] {0,1,4,9,16,25,36,…,81,100,121,144,…} 25+144=169
[1,0,2] {2,2,3,5,8,12,17,23,30,38,47,57,68,…} 12+ 68=80
───────────────────────────────────────────────────────────
Basic sequences
Basic sequence order k has F-sum with indexes (a,b,c) if
r0=
![]() −
−
![]() −
−
![]() .
.
It follows directly from transformation of sequences [0,0,0,...,0]
to [1,0,0,...,r0]
E.g. F-sum with indexes (0,2,5) exists in sequences with
characteristic [1,0,9], because
r0=
![]() −
−
![]() −
−
![]() = 10−1−0 = 9.
= 10−1−0 = 9.
Charakter. Sequence F-indexes F-sum
──────────────────────────────────────────────────────────
[1,0,9] {9,9,10,12,15,19,24,...} ( 0, 2, 5) 9+10=19
Binomial sequences
Sequence with characteristic [1,0,0] has members f(a)=
![]() .
.
Charakter. Posloupnost F-indexy F-součet
───────────────────────────────────────────────────────────
[1,0,0] {0,0,1,3,6,10,15,21,...} ( 4, 6, 7) 6+15=21
There is a Fermat-like question, for which (a,b,c) in
sequences of order k exist F-sums
![]() +
+
![]() =
=
![]() ?
?
For k=2 to 5 we get experimentally these indexes:
- k=2: (4,6,7),(5,10,11),(6,15,16),..(6,7,9),(7,10,12),(10,22,24),(11,27,29),... (9,11,14),(10,14,17),(12,21,24),...(12,15,19), ...
- k=3: (10,16,17),(22,56,57),(32,57,60),(36,120,121), ...
- k=4: (132,190,200),..?
- k=5: ?
E.g.
![]() +
+
![]() = 10 + 45 = 55 =
= 10 + 45 = 55 =
![]() .
.
Indexes in the first row are of the form (n,
![]() ,
,
![]() +1).
+1).
Shift of sequence
Change of characteristics r(m) by value v make shift of each
member of the sequence f(n) by value
![]() ∙v.
∙v.
We call the value m order of the shift.
E.g. for k=3 - members f(n) sequences [6,6,1,v] are
with regard to k sequences [6,6,1,0] shifted o value v∙
![]() = v:
= v:
Charakter. Sequence F-indexes F-sum
─────────────────────────────────────────────────────────
[6,6,1,0] {0,1, 8,27,64,125,216,..}
[6,6,1,1] {1,2, 9,28,65,126,217,..} ( 6,8,9) 217+513=730
[6,6,1,2] {2,3,10,29,66,127,218,..} ( 5,6,7) 127+218=345 Δ={1,1,1,1,1...}
Similarly are also members f(n) sequences [6,6,v,0] with
regard to k sequences [6,6,0,0] shifted by value v∙
![]() = v∙n:
= v∙n:
Charakter. Sequence F-indexes F-sum
──────────────────────────────────────────────────────────
[6,6,0,0] {0,0, 6,24,60,120,…} ( 9,15,16) 720+3360=4080
[6,6,1,0] {0,1, 8,27,64,125,…}
[6,6,2,0] {0,2,10,30,68,130,…} (36,37,46) 46692+50690=97382 Δ={0,1,2,3,4...}
And members f(n) of sequences [6,v,0,0] with regard to k
sequences [6,0,0,0] shifted by value v∙
![]() :
:
Charakter. Sequence F-indexes F-sum
──────────────────────────────────────────────────────────
[6,0,0,0] {0,0,0,6,24,60,… } ( 0, 1, 2) 0+0=0
[6,1,0,0] {0,0,1,9,30,70,… } (11,19,20) 1045+5985=7030
[6,2,0,0] {0,0,2,12,36,80,…} (31,37,43) 27900+47952=75852 Δ={0,0,1,3,6,10...}
Sequences of characteristics
The sequence of characteristics p = {r} is called a sequence of numbers r, which define the traced characteristics - usually for certain F-indices.
For example, we will observe which characteristics [1.0, r] have sequences with F-indices (0, b, c). For b = 2 we get the sequence p2 = {0,2,5,9,14,20,27,...}:
Charakter. F-indexy F-součet Posloupnost
──────────────────────────────────────────────────────────
[1,0,0] (0,2,2) 0+1=1 {0,0,1,3,6,10,15,21,28,...}
[1,0,2] (0,2,3) 2+3=5 {2,2,3,5,8,12,17,23,30,...}
[1,0,5] (0,2,4) 5+6=11 {5,5,6,8,11,15,20,26,33,...}
[1,0,9] (0,2,5) 9+10=19 {9,9,10,12,15,19,24,30,37,...}
[1,0,14] (0,2,6) 14+15=29 {14,14,15,17,20,24,29,35,42,...}
[1,0,20] (0,2,7) 20+21=41 {20,20,21,23,26,30,35,41,48,...}
[1,0,27] (0,2,8) 27+28=55 {27,27,28,30,33,37,42,48,55,...}
In general, for the F-indexes (0, b, c) we get characteristics [1,0,r], where r = [c2-c-(b2-b)]/2. The F-sum values are here: [(c2-c)/2-(b2-b)/2] + [(c2-c)/2] = [(c2-c)-(b2-b)/2]. E.g. for F-indexes (0,3,4) results r = [42-4-(32-3)]/2 = 6/2 = 3 a součet 3 + 6 = 9:
Charakter. F-indexes F-sum Sequence
──────────────────────────────────────────────────────────
[1,0,3] (0,3,4) 3+6=9 {3,3,4,6,9,13,18,24,31,39,48,...}
[1,0,7] (0,3,5) 7+10=17 {7,7,8,10,13,17,22,28,35,43,52,...}
[1,0,12] (0,3,6) 12+15=27 {12,12,13,15,18,22,27,33,40,48,57,...}
Limitation of characteristics of F-sums
We are interested, what properties must have sequences, in order to have any F-sum. Some cases are trivial; e.g. sequences of 0.order never have F-sum, except the case r0=0. I.e. in sequence 5,5,5,5,5,5,5.. can never appear an other number like 5+5 = 10, ....
In other cases we will observe influences of differential sequences existence of F-sums.
Sequences of 1.order
Any sequence of 1.order can be written in the form:
f(n) = r1∙n+ r0; where r0 = r1(c−b−a).
So F-sum exists, if number r0 is divisible by number r1 (with no
remainder):
Charakter. Sequence F-indexes F-sum
───────────────────────────────────────────────────────────
[1,0] {0,1,2,3,4,5,6,7,8,9,... } ( 1, 2, 3) 1+2=3
[1,1] {1,2,3,4,5,6,7,8,9,10,...} ( 0, 1, 2) 1+2=3
[1,2] {2,3,4,5,6,7,8,9,10,... } ( 0, 1, 3) 2+3=5
[1,3] {3,4,5,6,7,8,9,10,11,... } ( 0, 1, 4) 3+4=7
───────────────────────────────────────────────────────────
[2,0] {0,2,4,6,8,10,12,14,... } ( 1, 2, 3) 2+4=6
[2,1] {1,3,5,7,9,11,13,15,... }
[2,2] {2,4,6,8,10,12,14,16,... } ( 0, 1, 2) 2+4=6
[2,3] {3,5,7,9,11,13,15,17,... }
───────────────────────────────────────────────────────────
[3,0] {0,3,6,9,12,15,18,21,... } ( 1, 2, 3) 3+6=9
[3,1] {1,4,7,10,13,16,19,22,...}
[3,2] {2,5,8,11,14,17,20,23,...}
[3,3] {3,6,9,12,15,18,21,24,...} ( 0, 1, 2) 3+6=9
In sequences of 1.order can (potentially) exist F-sums only if:
r0 ≡ 0 (mod r1)
Sequences of 2.order
In sequences of 2.order we find similar formula:
r0≡0 mod (r1,r2)
where (r1,r2) is greatest common divisor of numbers r1 and r2.
E.g. for r1 = 6 we can distinguish following cases:
(r1,r2) F-sums exists for ──────────────────────────────────── (6,1)=1 all sequences (6,2)=2 r0≡0 mod 2 (6,3)=3 r0≡0 mod 3 (6,4)=2 r0≡0 mod 2 (6,5)=1 all sequences (6,6)=6 r0≡0 mod 6
Therefore:
In sequences [6,8,r0] F-sum exists if r0≡0 mod (6,8), i.e. when r0 is even:
Charakter. Sequence F-indexes F-sum
──────────────────────────────────────────────────────────
[6,8,0] {0,8,22,42,68,100,138,...} ( 4,10,11) 68+350=418
[6,8,1] {1,9,23,43,69,101,139,...}
[6,8,2] {2,10,24,44,70,102,140,..} ( 3, 6, 7) 44+140=184
[6,8,3] {3,11,25,45,71,103,141,..}
[6,8,4] {4,12,26,46,72,104,142,..} ( 2, 3, 4) 26+46= 72
[6,8,5] {5,13,27,47,73,105,143,..}
[6,8,6] {6,14,28,48,74,106,144,..} ( 4,11,12) 74+424=498
Charakter. Sequence F-indexes F-sum
──────────────────────────────────────────────────────────
[6,6,0] {0,6,18,36,60,90,126,... } ( 3, 5, 6) 36+90=126
[6,6,1] {1,7,19,37,61,91,127,... }
[6,6,2] {2,8,20,38,62,92,128,... }
[6,6,3] {3,9,21,39,63,93,129,... }
[6,6,4] {4,10,22,40,64,94,130,...}
[6,6,5] {5,11,23,41,65,95,131,...}
[6,6,6] {6,12,24,42,66,96,132,...} ( 2, 3, 4) 24+42=66
Charakter. Sequence F-indexes F-sum
──────────────────────────────────────────────────────────
[6,7,0] {0,7,20,39,64,95,132,..} ( 7,28,29) 175+2464=2639
[6,7,1] {1,8,21,40,65,96,133,..} ( 6,21,22) 33+1408=1541
[6,7,2] {2,9,22,41,66,97,134,..} ( 5,15,16) 97+737= 834
[6,7,3] {3,10,23,42,67,98,135,.} ( 4,10,11) 67+343= 410
More general criterion
Let us write more general relation for F-sum f(a)+f(b)=f(c) with help of characteristic of sequences.
E.g.
f(a)=r0∙
![]() +
r1∙
+
r1∙
![]() +
r2∙
+
r2∙
![]() + … = r0+
r1∙a+ r2∙a(a−1)/2+…
+ … = r0+
r1∙a+ r2∙a(a−1)/2+…
After an arrangement, an expressions dependent on (c−b−a),(c²−b²−a²) ... appear
To simplify these expressions, let use define function d(m):
d(m) = cm−bm−am
E.g. for sequence of the 3. order we get relation:
r0 +
r1∙d1 + r2(d2−d1)/2 +
r3(d3−3d2−2d1)/6 = 0
If some number divide numbers r1,r2,r3,... it must divide also the number r0, otherwise the previous relation is impossible.
F-sums can exist only in sequences if it holds:
r0≡ 0 mod (r1,r2,r3,...)
Zero members r1,r2,r3,... have to be skipped in calculation of greatest common divisor (r1,r2,r3,...).
In sequences with characteristic [2,0,1] can not exist F-sum, because it does not hold 1 ≡ 0 mod 2:
Charakter. Sequence Note
───────────────────────────────────────────────────────
[2,0,1] {1,1,3,7,13,21,31,43,...} f(n) = n²−n+1
But to validity of the Fermat’s theorem this criterion brings nothing new. For sequences f(k) = ak is always r0 = 0.
Qualification of indexes of F-sums
Transformation to zero sequences
Zero sequence contains F-sums with any indexes. Therefore, if F-sums exist in some given sequence, there exist F-sums also in the corresponding zero sequence.
And (vice versa) in sequences can exist F-sum with indexes (a,b,c) only if it can be derived from zero sequences by transformation for given (a,b,c).
E.g. in sequences [2,0,1] no F-sum can exists, because there does not exists any (a,b,c) for transformation from [0,0,0] to [2,0,1].
For existence of such transformation is needed:
2∙(
![]() −
−
![]() −
−
![]() )=1, i.e. (c²−c)
−(b²−b) −(a²−a)=1. But number m²−m
is even for all mεZ.
)=1, i.e. (c²−c)
−(b²−b) −(a²−a)=1. But number m²−m
is even for all mεZ.
But these relations are not distinct from those, that was deduced with help of breakdown of f(a)+f(b)=f(c) in previous paragraphs,
so they do not provide nothing new about power
sequences.
E.g. transformation [0,0,0] to [2,1,0] for (a,b,c) leads to
c²−a²−b²=0, which is
evident.
Transformation to basic sequences
Let us try to find basic sequences, that have F-sums with indexes equal to indexes in given power sequences.
Let us assume, that if basic sequence to given sequences having F-sum with indexes (a,b,c) does not exists,
then in given sequence the F-sum (a,b,c) is not possible.
In sequences of the 2.order it follows from transformation of
[2,1,0] to [1,0,r0]:
2∙r0 = (c²−b²−a²) − (c−b−a) = d2−d1
Because simultaneously d2=0 (i.e. a²+b²=c²) then:
2∙r0 = −d(1) = −d(1) = −(c−b−a) = a+b−c
Therefore it must hold for indexes F-sums of power sequences
of 2.order:
−d1 ≡0 mod 2 i.e. j+i−c≡0 mod 2
This formula holds in Pythagorean triangles, e.g. 3+4−5≡0 mod 2, 5+12−13≡0 mod 2, ...
We will find similar formulas for higher orders:
Order Formula ─────────────────────────────────────────── 2 −d1 ≡0 mod 2 3 −3∙d2+2∙d1 ≡ 0 mod 6 4 −6∙d3+11∙d2−6∙d1 ≡ 0 mod 24 5 −10∙d4+35∙d3−50∙d2+24∙d1 ≡ 0 mod 120
Numbers u of particular d(m) are Stirling’s numbers of the first case s(k,m), see Recurrent sequences.
More general criterion
To any power sequence of k-th order with indexes of F-sum (a,b,c)
there always exists one basic sequence with characteristic [1,0,...,0,r0], if it holds k!∙r0 = ∑ s(k,m)∙d(m), where d(m)=cm−bm−am.
Therefore it must hold for indexes of F-sum (a,b,c) in power sequences k-th order:
∑ s(k,m)∙d(m) ≡ 0 (mod k!)
In opposite case there corresponding basic sequence does not exists.
E.g. indexes (1,2,4) can not be solution of a³+b³=c³ because:
d1= c−b−a= 4−2−1 = 1,
d2= c²−b²−a²= 16−4−1= 11, −3∙d2+2∙d1 = −33+2 = −31
and −31 is not divisible by 6 (i.e. not congruent to 0 according to module k!=3!=6).
We can rewrite the said relations also to the form:
δc− δb− δa ≡0 mod k! where δa = a(a−1)(a−2)..(a−k+1).