Schematic algebra - Nesting
Nesting of G-systems
Self and nested classes
For each d|k there exists system G(n,d) nested into G(n,k). Nested class g' v G(n,k) is similar to original class g from G(n,d). (Similarity is given by the same number of transpositions and an analogous inner structure of instances). Really-original classes are called self classes. System G(n,p), p is prime, has just one nested system G(n,1).
For g from G(n,d), g' from G(n,k), d|k it holds: g' = c . g where c is quotient of nesting defined:
c(k,d) = (nk−1) / (nd−1)
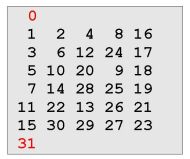
Into system G(2,4) systems G(2,1) a G(2,2) nests.
E.g. class g(2) = 1 from G(2,2) enter into G(2,4) as g(4) = 5 with quotient of nesting c(2,4) = 5:
G(2,1):
g(1)=u(0,1)= 0
g(2)=u(0,2)= 1
G(2,2):
g(1)=u(0,1)= 0
g(2)=u(0,2)= 1 u(1,2)= 2
g(3)=u(0,3)= 3
|
G(2,4):
g(1)=u(0,1)= 0
g(2)=u(0,2)= 1 u(1,2)= 2 u(2,2)= 4 u(3,2)= 8
g(3)=u(0,3)= 3 u(1,3)= 6 u(2,3)=12 u(3,3)= 9
g(4)=u(0,4)= 5 u(1,4)=10
g(5)=u(0,5)= 7 u(1,5)=14 u(2,5)=13 u(3,5)=11
g(6)=u(0,6)=15
|
Coefficients of nesting:
G(2,1) − G(2,2): c(1,2) = (2² −1) / (21 −1) = 3
G(2,2) − G(2,4): c(2,4) = (24 −1) / (2² −1) = 5
 Litle Fermat theorem
Litle Fermat theorem
System G(n,k) has nk instances. All classes g relative prime to r=nk−1 (i.e. (g,r)=1) are self-classes. Into system G(n,p), p ε P, n instances (from G(n,1)) are nested . All other instances are self and have k transpositions. Therefore so called Little Fermat’s theorem holds for integers n: p\(np−n), i.e.:
np − n ≡ 0 (mod p)
Euler (1736) was the first who proved little Fermat theorem. On the picture is G(2,5), where 5 \ (25−2) i.e. 5 \ 30.
From Little Fermat’s theorem a similar theorem for cyclical
numbers follows:
(2³−2)+(5³−5)α³ ≡ 0
(mod 3) => (2+5α)³ −(2+5α³) ≡ 0 (mod 3)
Enumeration of classes
Problem of enumeration of classes was solved by K.F.Gauss in algebraic theory of equation classes [Gauss,II]. Polya has shown combinatorial solution – he derived theorem for enumeration of classes with regard to given operations of symmetry [Preparata,1974]. G-systems are based on one operation only – rotation. That makes possible to use simpler and more transparent algebraic relations.
Let v(n,k), w(n,k) a m(n,k) are numbers of self, nested and all classes in G(n,k).
Recurrent relations:
M(n,k) = v(n,k) + w(n,k)
wherev(n,k) = (nk−∑ d∙v(n,d))/k (sum for d\k)
andw(n,k) = ∑ v(n,d) (sum for d\k)
Specially for prime order p:
M(n,p) = (np + (p−1)∙n)/p
v(n,p) = (np − n)/p
w(n,p) = n
System G(2,6)Systems G(2,1), G(2,2) a G(2,3) are nested into systems G(2,6) , G(2,1) is nested also into G(2,2) a G(2,3).
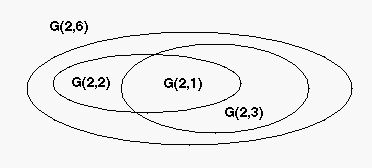
From total 14 classes 9 classes are self and 5 are nested.
Self classes Nested classes ───────────────────────────────────────────────────────────────────────────────── v(2,1)=2/1=2 w(2,1)= 0 v(2,2)=(2²−v(2,1))/2=1 w(2,2)= v(2,1) = 2 v(2,3)=(2³−v(2,1))/3=2 w(2,3)= v(2,1) = 2 v(2,6)=(26−v(2,1)−2∙v(2,2)−3∙v(2,3))/6=9 w(2,6)=v(2,1)+v(2,2)+v(2,3)= 5
Therefore m(2,6)= v(6) +w(6) = 9 +5 = 14 classes.
Numbers of self classes
Numbers of self classes v(n,k) written as functions of variable n:
k v(n,k)
─────────────────────────────────────
1 1/1(n) = n
2 1/2(n²−n)
3 1/3(n³−n)
4 1/4(n4−(n²−n)−n)=¼(n4−n²)
5 1/5(n5−n)
6 1/6(n6−(n³−n)−(n²−n)−n)=1/6(n6−n³−n²+n)
7 1/7(n7−n)
8 1/8(n8−(n4−n²)−(n²−n)−n)=1/8(n8−n4)
9 1/9(n9 −n³)
10 1/10(n10−n5−n²+n)
11 1/11(n11−n)
12 1/12(n12−n6−n4+n²)
13 1/13(n13−n)
|
1 2 3 4 5 6 7 8
──────────────────────────────────────────
1 2 3 4 5 6 7 8
0 1 3 6 10 15 21 28
0 2 8 20 40 70 112 168
0 3 18 60 150 315 588 1008
0 6 48 204 624 1554 3360 6552
0 9 116 670 2580 7735 19544 43596
0 18 312 2340 11160 39990 117648 299592
0 30 810 8160 48750 209790 720300 2096640
0 56 ...
0 99 ...
0 186 ...
0 335 ...
0 ...
|
For prime p is:
v(p,p) = pp−1−1
i.e. v(p,p)≡−1 mod p. Quotient v(n,p)/n (pεP) corresponds to Fermat’s quotients.
Numbers of nested classes w(n,k) written as functions of variable n:
k w(n,k) ───────────────────────────────────── 1 0 2 n 3 n 4 1/2(n²−n)+1/1(n)= 1/2(n²+ n) 5 n 6 1/3(n³−n)+1/2(n²−n)+1/1(n)=1/6(2n³+3n²+n) 7 n 8 1/4(n4−n²)+1/2(n²−n)+n = 1/4(n4+n²+2n) |
1 2 3 4 5 6 7 8 ───────────────────────────────────── 0 0 0 0 5 6 7 8 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 1 3 6 10 15 21 28 36 1 2 3 4 5 6 7 8 1 5 14 30 55 91 140 204 1 2 3 4 5 6 7 8 1 6 24 70 165 336 616 1044 |
Let us unfold given recurrent relations for number of all classes. Numbers of all classes m(n,k) written as functions of variable n:
k m(n,k) ───────────────────────────────────────── 1 1/1(n) + 0 = n 2 1/2(n²− n)+ n = 1/2 (n²+n) 3 1/3(n³−n)+ n = 1/3 (n³+ 2n) 4 1/4(n4−n2)+ 1/2 (n²+n)=1/4 (n4+ n²+2n) 5 1/5(n5−n) + n = 1/5 (n5+ 4n) 6 1/6(n6−n³−n²+n+2n³+3n²+n)=1/6(n6+n³+2n²+2n) 7 1/7(n7−n) + n = 1/7 (n7+ 6n) 8 1/8(n8−n4)+1/4(n4+n²+2n)=1/8(n8+n4+2n²+4n) |
1 2 3 4 5 6 7 8 ───────────────────────────────────────── 1 2 3 4 5 6 7 8 1 3 6 10 15 21 28 36 1 4 11 24 45 76 119 176 1 6 24 70 165 336 616 1044 1 8 51 208 629 1560 3367 6560 1 14 130 700 2635 7826 19684 43800 1 20 315 2344 11165 39996 117655 299600 1 36 834 8230 48915 210126 720916 209768 |
Expressions in brackets on the right (n, n²+n, n³+ 2n, n5+ 4n,..) have no absolute member, therefore it holds:
k∙m(n,k) ≡ 0 (mod n)
For prime p it holds:
m(p,p) = pp−1+p−1
i.e. m(p,p)≡−1 mod p.
Differential sequences v G-systemech
Sequences v(n,k) and m(n,k) (n=1,2,3..) makes for any k
arithmetical sequences of order k.
Value of constant of the last differential sequences is:
· For v(n,k): d(k) = (k−1)!
· For m(n,k): d(k) = k!
The first differential sequence m(n,k) is similar to sequences nk−1.
m(n,3) n² ──────────────────── ────────────────── 1,4,11,24,45,76,... ....... 3,7,13,21,31,... 1,4,9,16,25,36,... 4,6, 8,10,... 3,5,7,9,11,.. 2,2,2,,.... 2,2,2,2,...
Orders k as well as constant d(k) of these sequences are equal.
For number of self classes in G-system G(p) it holds:
v(p,i+p) + (−1)p ∙ v(p,i) ≡ −1 (mod p)
E.g. for p = 5, a(i)=v(5,i): a(0) = 0; a(1) = 6; a(2) = 48;
a(3) = 204; a(4) = 624; a(5) = 1554;
i.e. a(5)−a(0)= 1554 ≡ (−1) mod 5 (see periodic
sequences).
| Messiaen Olivier [], 1908-1992, French composer of mystical music with expressive melodies. He worked with the modalities which have a limited number of transpositions. |
There are 17 classes nested into system G(2,12) and
2∙1+1∙2+2∙3+3∙4+9∙6 = 76 instances in these classes.
System Distance schema Example Name
────────────────────────────────────────────────────────────────────────
G(2,1):
0 0(0) Silence
4095 11111…1(1) c,c#,d,d#,e,…,a#,h 12-sound
G(2,2):
1365 22222(2) c,d,e,f#,g#,a# Wholetone scale
G(2,3):
585 333(3) c,d#,f#,a Diminished tetrad
1755 1212121(2) c,c#,d#,e,f#,g,a,a# Inverse dim. tetrad
G(2,4):
273 44(4) c,e,g# Augmented triad
819 13131(3) c,c#,e,f,g#,a
1911 11211211(2) c,c#,d,e,f,f#,g#,a,a# Inverse augm. triad
G(2,6):
65 6(6) c,f# Tritonus
195 151(5) c,c#,f#,g .
325 242(4) c,d,f#,g# ..
455 11411(4) c,c#,d,f#,g,g# Messiaen‘s modes
715 12312(3) c,c#,d#,f#,g,a of limited transpositions
845 21321(3) c,d,d#,f#,g#,a ...
975 1113111(3) c,c#,d,d#,f#,g,g#,a ..
1495 1122112(2) c,c#,d,e,f#,g,g#,a# .
2015 111121111(2) c,c#,d,d#,e,f#,g,g#,a,a# Inversion of tritone
| Janeček Karel, 1903-1974, Czech music theorist and composer (creator of piano, chamber, vocal and orchestral music). One of the biggest Czech music theorists, systematist. He was interested in the theory of composition and in harmony of music, both classical and modern. Systematically listed all possible chords of 12-tone system and rated it by several characteristics. He devoted to musical tectonics, to musical forms, to the theory of melody, to analyze of musical compositions and also to issues of compositional imagination, talent ... He generalized and precisely formulated thoughts of his predecessors and documented principles by excerpts from the musical works. |
Number of chord classes
From relations above we in case n=2 get these values:
k v(2,k) w(2,k) m(2,k) ────────────────────────── 1 2 0 2 2 1 2 3 3 2 2 4 4 3 3 6 5 6 2 8 6 9 5 14 7 18 2 20 8 30 6 36 9 56 4 60 10 99 9 108 11 186 2 188 12 335 17 352
There is 4096−76=4020 self instances, i.e. groupings having all 12 transpositions in 12-tone musical system. These instances make 4020/12 = 335 classes. Therefore there is together 335+17 = 352 classes in 12-tone musical system.
Number of classes in large systems
In small systems G(2,k) number of classes corresponds
approximately to number of possibilities p(k) to partition number k
into sum of positive integers (see Partition of numbers into
sums):
m(2,k) ~ p(k)
E.g. system G(2,4) (see Binary G-systems/ Distance schemas)
is composed of classes corresponding to sums:
4,3+1,2+2,2+1+1,1+1+1+1 and of zero class.
For higher value k, number m(2,k) grows more quickly
than p(k).
E.g. in G(2,6) sum 2+2+1+1 decay into two classes: 1,2,1,2 and
1,1,2,2. Therefore m(2,k) > p(k).
To estimate number of classes in larger G-systems we will try to apply prime-number theorem.
For bigger r it holds approximately:
π(r) = r/ln(r), π(r)∙ln(r) =
r, eln(r)∙π(r) = er
(eln(r))π(r) =
er, rπ(r) = er
i.e.:
r ~ ln(rπ(r))
Now let us consider case r=nk. After substitution
and computation of k-th radical:
rπ(r) = er,
(nk)π(nk) =
e(nk), n(k∙π(nk)) =
e(nk),
nπ(nk) =
e(nk/k)
The expression nk/k gives for higher r approximately number of all classes m in system G(n,k).
So it holds approximately:
nπ(r) =
em, ln(nπ(r)) = m
m ~ π(r)∙ ln(n)
where n is base, r module and m number of classes in system G(n,k).
E.g. for n=10, k=3, i.e. r=1000 a π(r)=168. Raw estimate for number of classes in G(10,3) is m=π(r)∙ ln(n)=168 ∙ ln(10) = 387.
Polya‘s enumeration
Polya’s enumeration determines number of possible partitions of given set into classes of equivalence. It was applied to chemical structures…
It enables computation of numbers of equivalence classes.
Method of computation
Method of determination of total number of classes according to Polya’s theory:
· to select operations of symmetry (rotation, inverse, axial symmetry,...)
· to find number of fixed instances for each operation, i.e. instances that stay (after application of the operation) unchanged (fixed)
· to assembly (according to given rules) so called cycle index (polynomial of cycles),
· to set values into cycle index, result gives total number of classes
Polya’s theory in case of rotation gives result [Beckenbach]:
m(n,k)=1/k ∑φ(d)∙ nk/d for d|k, d≤k
where φ is Euler function.
Pólya, Győrgy| Pólya, Győrgy [poja], 1887-1985 Hungarian mathematician of liberal education and personal style of interpretation. His mathematical work is extensive and affects a wide range of disciplines. Well known is his enumeration theorem of 1937. He studied the methods of teaching mathematics. |
The base of the relation is the following schema of fixed instances:
0 * * * 1 2 4 8 3 6 12 9 5 10 * * 7 14 13 11 15 * * *
Existing instances (given by numbers) are completed by these marked by asterisk (i.e. the sum on the right side).
All S instances make rectangle having width k and height m, therefore m = S/k.
Value m(n,k) (i.e. total number of classes) is called (in Polya’s theory) number of cyclical permutations of k-th class from n elements with repetition.
Characteristics of permutations
Polynomial composed of cycle type is indicator of permutation cycles. Length d of each cycle is index and number of cycles p of given length is exponent of expression (xdp).
Indicator of cycles of group I(x) is sum of indicators of particular permutations.
E.g. elements of permutation groups of 3 degree have the following characteristics:
Permutation Cycle and order Lengths Parity Type and indicator
──────────────────────────────────────────────────────────────
p0 123 (1)(2)(3) 1 1 1 even (+) (3,0,0)
123 1 x1³
──────────────────────────────────────────────────────────────
p1 123 (1) (2,3) 1 2 odd (−) (1,1,0)
132 2 x11+x21
──────────────────────────────────────────────────────────────
p2 123 (1,2,3) 3 even (+) (0,0,1)
231 3 x31
───────────────────────────────────────────────────────────────
p3 123 (2) (1,3) 1 2 odd (−) (1,1,0)
321 2 x11+x21
───────────────────────────────────────────────────────────────
p4 123 (1,3,2) 3 even (+) (0,0,1)
312 3 x31
──────────────────────────────────────────────────────────────
p5 123 (3) (1,2) 1 2 odd (−) (1,1,0)
213 2 x11+x21
Indicator of cycles
We mark in case of permutation group indicator of cycles
T(x).
For P(3) is:
T3(x)= (x1³)+
(x11 +x21)+
(x31)+ (x11
+x21)+ (x31) +
(x11 +x21)
i.e.T3(x) = x1³ +
3x1x2 + 2x3
Generally for P(k) we get the following relations:
T1(x) = x1
T2(x) = x1² + x2
T3(x) = x1³ +
3x1∙x2 + 2x3
T4(x) = x14 +
6x1²∙x2 +
3x2² + 8x1∙x3 +
6x4
T5(x) = x15 +
10x1³∙x2
+15x1∙x2²
+20x1²∙x3 +
20x2∙x3 + 30x1∙x4 +
24x5
Coefficients of these polynomials come from so called Cauchy’s formula (se below).
Derivation of indicator of cycles
For partial derivation of given polynomials according to
x1,x2,.. some relations hold.
Let us compute partial derivations of indicator of cycles in
P(3):
d(x1³ +
3x1∙x2 + 2x3)/ dx3 =
2
[=(3−1)!]
d(x1³ +
3x1∙x2 + 2x3)/ dx2 =
3x1 [=3∙(3−2)!x1]
d(x1³ +
3x1∙x2 + 2x3)/ dx1 =
3x1²+ 3x2
[...]
Generally it holds e.g. [Riordan]:
dT(x)/dxn = (n−1)!
dT(x)/dxn−1 = n∙(n−2)!x1
Cyclic index
Sum of indicators of particular permutations is (in our example of rotations) P(x) = x1³ + 2∙x31 (see even permutation in the previous table).
Mentioned permutations keep sequences of elements 1−2−3−1−... and therefore correspond to rotations (G-systems are based on rotations).
According to Polya’s enumeration is number of classes determined by so called cycle index.
Cycle index of group M(x) is cycle indicator of group divided by order of group, i.e.
M(x) = P(x)/k
where k is number of operations of symmetry. In our example we have three rotations (k=3). Then number of elements (n) will be substituted to x.
So in G(n,3) twe get: m(n,3) = (n³ + 2∙n)/3.
For n=2 resp.3 is therefore: m(2,3) = (8+4)/3 = 4, resp. m(3,3) = (27+6)/3 = 11.
This result corresponds to values obtained by recurrent algorithm of G-systems (see paragraph Enumeration of classes/Number of all classes).
Nature of enumeration
Partition of elements in k-apexes is fixed with regard to certain operation, if each apex keep (after application of this operation) the same element as before. In the given relation m(n,3) = (n³ + 2∙n)/3 determine fixed instances the term 2∙n.
There are 4 fixed instances (marked by asterisks) in system G(2,3):
0 * * 1 2 4 3 6 5 7 * *
Composition of R-systems
R-systems with given module
For prime module there exist always two trivial systems and several pairs of dual systems.
E.g. for r=13 we have trivial systems R(1,1,13), R(12,2,13) and dual systems with degrees nε{1..r−1} written below (ordered by k)
k=3
R(3,3,13) R(9,3,13)
0 0
1 3 9 1 9 3
2 6 5 2 5 6 φ(3)=2
4 12 10 4 10 12
7 8 11 7 11 8
13 13
R(5,4,13) R(8,4,13)
0 0
1 5 12 8 1 8 12 5
2 10 11 3 2 3 11 10 φ(4)=2
4 7 9 6 4 6 9 7
13 13
R(4,6,13) R(10,6,13)
0 0
1 4 3 12 9 10 1 10 9 12 3 4
2 8 6 11 5 7 2 7 5 11 6 8 φ(6)=2
13 13
R(2,12,13)
0
1 2 4 8 3 6 12 11 9 5 10 7
13
R(6,12,13)
0
1 6 10 8 9 2 12 7 3 5 4 11
13 φ(12)=4
R(7,12,13)
0
1 7 10 5 9 11 12 6 3 8 4 2
13
R(11,12,13)
0
1 11 4 5 3 7 12 2 9 8 10 6
13
The highest order for prime rεP is k= r−1.
Orders of particular systems are numbers k, that divide number r−1: k|(r−1). In our case these are divisors of numbers 12, i.e. 1,2,3,4,6 and 12.
Number of systems with given order k is φ(k):
k 1 2 3 4
6 12
φ(k)
1 1 2 2 2 4
Permutations of R-systems
All systems of the same order are similar. Numbers in rows does not change, they only reorder.
E.g. systems R(3,3,13) and R(9,3,13) differ only in
order of the second and third column.
R(3,3,13):
R(9,3,13):
0
0
1 3
9
1 9
3
...
...
Reordering of number {1,3,9} and {1,9,3} is composed of two cycles: one elementary (length 1) and one of length 2.
This permutation we will write symbolically [1][3,9].
Similarly for next orders k:
R(3,3,13): 1 3 9 k = 3
R(9,3,13): 1 9 3
cycles: [1][3,9]
───────────────────────────────────
R(5,4,13): 1 5 12 8 k = 4
R(8,4,13): 1 8 12 5
cycles: [1][12][5,8]
───────────────────────────────────
R( 4,6,13): 1 4 3 12 9 10 k = 6
R(10,6,13): 1 10 9 12 3 4
cycles: [1][12][3,9][4,10]
───────────────────────────────────────────────────────────
R( 2,12,13): 1 2 4 8 3 6 12 11 9 5 10 7
R( 6,12,13): 1 6 10 8 9 2 12 7 3 5 4 11 k = 12
R( 7,12,13): 1 7 10 5 9 11 12 6 3 8 4 2
R(11,12,13): 1 11 4 5 3 7 12 2 9 8 10 6
cycles: [1][12][3,9][5,8][4,10][2,6,11,7]
Theorem about composition of R-systems
Let d is divisor of order k, d|k. Cycles in system R(n,d,r)
are subsets of cycles R(n,k,r).
E.g. [1][3,9] (d=3) is subset [1][12][3,9][4,10] (k=6) because
d|k.
Numbers in brackets are bases of systems being permutated.
They contains bases of nested systems and also self permutation of
bases of given order.
For k=12 there exists nested permutation [1][12][3,9][5,8][4,10] a
self permutation [2,6,11,7].
| Euler, Leonard [ojler], 1707-1783, Swiss mathematician and physicist, one of the greatest mathematicians of all time. He was interested in theoretical mathematics and its applications (mechanics, astronomy, optics, cartography, music theory ...) He studied number theory, differential, integral calculus and calculus of variations. Discovered a method of solving biquadratic equation. He affected all areas of mathematics, often by a quite original way. Many symbols introduced by him are still in use (i = √-1, Σf(x), ...). After blindness in y.1766 he dictated his work. |
Because there is always only one self permutation, there is
σ(k) of particular cycles, where σ(k) is number of divisors of
numbers k.
For k=12 is σ(12) = 6 and the following permutations correspond to particular divisors:
d= 1: [1] φ( 1) = 1
d= 2: [12] φ( 2) = 1
d= 3: [3,9] φ( 3) = 2
d= 4: [5,8] φ( 4) = 2
d= 6: [4,10] φ( 6) = 2
d=12: [2,6,11,7] φ(12) = 4
Each self permutation of order k has just φ(k) elements.
Every element is base of one system.
For k=12 is φ(12) = 4:
R( 2,12,13): 2 6 11 7
R( 6,12,13): 6 2 7 11
R( 7,12,13): 7 11 6 2
R(11,12,13): 11 7 2 6
Values φ(d) particular divisors d|k compose gradually order k.
For k=12 is: φ(1)+φ(2)+φ(3)+φ(4)+φ(6)+φ(12) = 1+1+2+2+2+4 = r−1 =12.
Generally it holds (Euler-Gauss) theorem, that we will call theorem about composition of R-systems:
∑(φ(d)) = a; for d|a (d>0)
i.e. each number a is sum φ(d) of all its divisors.
Nesting of R-systems
Comparison with G-systems
Similarly as in G-systems also in R-systems set of all instances {0..r} is separated by congruence (G-relation) into classes.
There are also self and nested classes and similar rules of composition.
Let us start with example, when nεP and numbers r ar not multiples of n (i.e. not n|r) [Gauss II].
Let us have e.g. r=63 and let us compare R-system R(13,6,63) and G-system G(2,6)= R(2,6,63):
G(2,6)=R(2,6,63) R(13,6,63):
0 0
1 2 4 8 16 32 1 13 43 55 22 34
3 6 12 24 48 33 2 26 23 47 44 5
5 10 20 40 17 34 3 39
7 14 28 56 49 35 4 52 46 31 25 10
9 18 36 6 15
11 22 44 25 50 37 7 28 49
13 26 52 41 19 38 8 41 29 62 50 20
15 30 60 57 51 39 9 54
21 42 11 17 32 38 53 59
23 46 29 58 53 43 12 30
27 54 45 14 56 35
31 62 61 59 55 47 16 19 58 61 37 40
63 18 45
21
24 60
27 36
33 51
42
48 57
63
Modules of both systems (r=63) are the same. Why and in what these systems differ? What classes are nested into R(13,6,63)?
Principle of nesting
Nesting of G-systems is determined by quotient of nesting c(k,d)=(nk−1)/(nd−1) = r/(nd−1)
For G(2,6) is c(d,6)= r/(2d−1), where d=1,2 or 3. For R(13,6,63) but values (13d−1) number r=63 nedělí...
Number r=63 is divisible with value (13d−1) until
it is possible and it is decided by greatest common divisor
(r,13d−1):
(131−1,r)= (13−1,63) = (12,63) =
3
(13²−1,r)= (169−1,63) = (168,63) = 21
(13³−1,r)= (2197−1,63)= (2196,63)= 9
Into system R(13,6,63) the following 3 systems are nested:
r=3: (q=21) r=21: (q=3)
0 0
1 1 13
2 2 5
3 3 18
4 10
r=9: (q=7) 6 15
0 7
1 4 7 8 20
2 8 5 9 12
3 11 17
6 14
9 16 19
21
Quotient of nesting
We define quotient of nesting c(k,d) for nesting of systems with order d | k into R-system R(n,k,r):
c(k,d) = r / (nd−1,r)
In our example R(13,6,63) is:
c(6,1) = 63 /
(131−1,r) = 63/3 = 21
c(6,2) = 63 /
(13²−1,r) = 63/21 = 3
c(6,3) = 63 /
(13³−1,r) = 63/9 = 7
Nested instance
Započítáme-li do vnořovaných systems G(2,6) all instance,
i.e. i instance nested from lower systems we get:
for d=1: 21=2 instances: 0,63
for d=2: 2²=4 instances: 0,21,42,63
for d=3: 2³=8 instances:
0,9,18,27,36,45,54,63
|
If ν=63 a p=13, then m=6. Therefore x63−1 will have according to module 13 simple coefficients of the sixth, third, second and first degree. But power of factors of the first degree is a common divisor (of higher degree) of functions x63−1 and x12−1, i.e.x³−1. Therefore there exist 3 coefficients of the first degree. Product of all prime factors of the second and of the first degree will be common divisor of functions x63−1 and x168−1, i.e. equal to x21−1; so there exists (21−3)/2=9 members of second degree. Product of prime factors of the third and of the first degree will be common divisor of functions x63−1 a x2196−1, i.e. equal to x9 −1; so there exists (9−3)/3=2 members of the third degree. Finally the others are of sixth degree and their number is similarly equal to (63−6−18−3)/6, i.e. 6. |
In R(13,6,63) we find similarly:
for d=1: 4 instances:
0,21,42,63
for d=2: 22 instances:
0,3,6,9,12,...54,57,60,63
for d=3: 10 instances:
0,7,14,21,28,35,42,49,56,63
These are for d=1,2 resp. 3 multiples of 21,3 resp. 7.
Enumeration of number of classes
Method for enumeration of classes in systems R(n,k,r) [GaussII] follows
from the previous paragraph.
K.F.Gauss (in distinction from our convention) does not include number 0 into number of classes.
Nesting of M-systems
Case k=1M(4,3) 0 1 4 16 2 8 11 3 12 6 5 20 17 7 9 15 18 10 19 13 14 21
For k=1 is always r=(n1−1)/(n−1)=1 and all systems M(n,1) are the same, they have 2 instances {0,1}. But their nesting is not the same as in case of G-systems. System M(4,3), i.e. k=3 nests four instances {0,7,14,21} from the system M(4,1): Generally always w1 classes from M(n,1) nest into system M(n,k), where:
w1 = (n−1,k)+1
In case n=2 (G-systems) is w1 =(1,k)+1 = 1+1 = 2 (= n).
Nesting of M-systems M(n,d) with order d|k into system M(n,k) is analogous to nesting of G-systems only in case (n−1,k)=1.
In this case M-systems of lower orders d nests into M-systems
of higher order k:
M(4,1) → M(4,2) → M(4,4) → M(4,8)
M(3,1) → M(3,3) → M(3,9) ...
In case of prime k, M-system has all classes self, except 2
classes nested from system 1.
E.g. M(3,3)
0
1 3 9
2 6 5
4 12 10
7 8 11
13
It has therefore together (nk−1)/(n−1)+1−2 =(nk−1)/(n−1) −1 = (nk−n)/(n−1) self instances and (nk−n)/(n−1)/k self classes.
0
13 65
26 130
39
52 104
78
91 143
117
156
If condition (n−1,k)=1 is not satisfied, then into given M-system nests generally other number of classes than any M-system can have. In some trivial cases is M-system M(n,d) replaced by G-system G(n,d)
E.g. M(3,2) + G(3,3) M(3,6), G(4,2) + M(4,3) => M(4,6).
But generally - nested structure needn’t to have form of neither M-system nor G-system.
E.g. M(5,4) has 13 nested classes, that doesn’t make neither M system M(5,2), having (5²−1)/(5−1)+1 = 24/4+1 = 7 instances nor G-system G(5,2) having 5² = 25 instances.
Quotient of nesting
In our example of classes nested into system M(5,4), we can see, that classes from system of order k= 1 nest with quotient c(4,1)= 39 and classes from system of order k= 2 with quotient c(4,2)= 13.
From this we guess relation like:
c(k,d)= (nk−1)/(nd−1)/(n−1,k/d)
In our case:
c(4,1)= (54−1)/(51−1)/(5−1,4/1)
= 624/4/(4,4) = 624/16 = 39
c(4,2)= (54−1)/(5²−1)/(5−1,4/2)
= 624/24/(4,2) = 624/48 = 13
In chapter abou R-systems we have formulated Gauss' general relation for quotient of nesting:
c(k,d) = r / (nd−1,r)
For M-systems is r = (nk−1)/(n−1).
In our case is r = (54−1)/(5−1) = 624/4 = 156.
c(4,1)= r/(51−1,r) = 156/(4,156) = 156/4 = 39
c(4,2)= r/(5²−1,r) = 156/(24,156) = 156/12 = 13
Comparison
Now (from the previous paragraph) we have two relations for
quotient of nesting. If they both were true, the following relation
follows:
(nk−1)/(nd−1)/(n−1,k/d) =
(nk−1)/(n−1)/(nd−1,(nk−1)/(n−1))
i.e. (n−1,k/d) = (nd−1,(nk−1)/(n−1)) / ((nd−1)/(n−1)).
Let us mark r(i) = (ni−1)/(i−1) and rewrite this relation to form:
(nd−1, r(k)) = r(d)∙(n−1,k/d)
Enumeration of classes
System M(3,6) has these nested classes from systems M(n,d), d|k:
0
14 42 126
28 84 252
56 168 140
70 210 266
91 273
98 294 154
112 336 280
182
196 224 308
238 350 322
364
Total m1=(n−1,k)+1 = (2,6)+1 = 3 instances i.e. 3 classes with one transposition
come from the system of order d=1:
0
182
364
For system of order d=2 is value t=(n−1)/(n−1,k/d) =2/(2,3) =
2. Nested schema has altogether m2= (nd−1)/t+1 =
(3²−1)/2+1 = 5 instances:
0
91 273
182
364
Because t=n−1, nested schema makes M-system M(3,2). But three instances became (as we have seen above) to system of order d=1. Therefore we add only 5−3=2 new instances, that makes 2/d = 1 class.
0
14 42 126
28 84 252
56 168 140
70 210 266
98 294 154
112 336 280
182
196 224 308
238 350 322
364
In system of order d=3 is parameter t=(n−1)/(n−1,k/d) =2/(2,2) = 1. Nested schema has altogether m3= (nd−1)/t+1 = (3³−1)/1+1 = 27 instances.
Because t=1, make nested schema G-system G(3,3). But again three instances are from system of order d=1. So we add 27−3=24 new instances, that make 24/d = 8 classes. Now we know, that into system M(3,6) come 3+1+8 = 12 classes, that make 3∙1 + 1∙2 + 8∙3 = 3+2+24 = 29 instances. Given M-system has altogether m6 = (nk−1)/(n−1)+1 = (36−1)/2+1 = 365 instances. (We needn’t compute the parameter t, in case of M-system it is always t=n−1.) After subtraction of nested instances we get 365−29 = 336 instances separated into 336/k = 56 classes. System M(3,6) has therefore 56 self and 12 nested classes, i.e. altogether 68 classes.
Number of classes
v(n):
k\n 1 2 3 4 5 6 7 8
─────────────────────────────────────────────────
1
2 1 1 2 2 3 3 4
3 2 4 6 10 14 18 24
4 3 8 20 36 63 96 144
5 6 24 68 156 310 560 936
6 9 56 222 640 1547 3246 6228
w(n):
k\n 1 2 3 4 5 6 7 8
─────────────────────────────────────────────────
1
2 2 3 2 3 2 3 2
3 2 2 4 2 2 4 2
4 3 6 4 9 5 10 6
5 2 2 2 2 6 2 2
6 5 12 16 25 19 52 30
m(n):
k\n 1 2 3 4 5 6 7 8
─────────────────────────────────────────────────
1
2 3 4 4 5 5 6 6
3 4 6 10 12 16 22 26
4 6 14 24 45 68 106 150
5 8 26 70 158 316 562 938
6 14 68 238 665 1566 3298 6258
Nesting of F-systems
Self classes
Self classes in F-systems have 2h transpositions. (Therefore we use from the beginning letter h in exponent instead of k).
For order k of F-system F(n,h)= R(n,k,r) it holds:
k=2h
System R(n,k,r) cannot have more than φ(r) transpositions, therefore 2h ≤ φ(nh+1).
Systems with exponent h=2t
There exists w = 2+(n mod 2) nested classes in these systems.
Systems with prime exponents
w = 2+ (n+1) div 2
Into systems with prime h this number of classes nests:
v = (nh−n)/2h
Number of self classes:
E.g. v F(2,11) is n=2, h=11 a r=211+1 = 2049. Into system w = 2+ (n+1) div 2 = 2 + 1 = 3 classes are nested. And there is v = (nh−n)/2h = (2048−2)/22 = 93 self classes.
Systems with prime module
If r=(nh+1) ε P then:
w = 2
v = nh/2h
Therefore for (n,h)= 1 can never be rεP.Nesting of multiplicative tables
Multiplicative tables
Tables T(k) of numbers m*n mod k, e.g.:
T1 T2 T3 T4 T5
1 1 2 1 2 3 1 2 3 4
2 1 2 0 2 2 4 1 3
3 2 1 3 1 4 2
4 3 2 1
T6 T7 T8
1 2 3 4 5 1 2 3 4 5 6 1 2 3 4 5 6 7
2 4 0 2 4 2 4 6 1 3 5 2 4 6 0 2 4 6
3 0 3 0 3 3 6 2 5 1 4 3 6 1 4 7 2 5
4 2 0 4 2 4 1 5 2 6 3 4 0 4 0 4 0 4
5 4 3 2 1 5 3 1 6 4 2 5 2 7 4 1 6 3
6 5 4 3 2 1 6 4 2 0 6 4 2
7 6 5 4 3 2 1
T9 T10
1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9
2 4 6 8 1 3 5 7 2 4 6 8 0 2 4 6 8
3 6 0 3 6 0 3 6 3 6 9 2 5 8 1 4 7
4 8 3 7 2 6 1 5 4 8 2 6 0 4 8 2 6
5 1 6 2 7 3 8 4 5 0 5 0 5 0 5 0 5
6 3 0 6 3 0 6 3 6 2 8 4 0 6 2 8 4
7 5 3 1 8 6 4 2 7 4 1 8 5 2 9 6 3
8 7 6 5 4 3 2 1 8 6 4 2 0 8 6 4 2
9 8 7 6 5 4 3 2 1
T11 T12
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 11
2 4 6 8 10 1 3 5 7 9 2 4 6 8 10 0 2 4 6 8 10
3 6 9 1 4 7 10 2 5 8 3 6 9 0 3 6 9 0 3 6 9
4 8 1 5 9 2 6 10 3 7 4 8 0 4 8 0 4 8 0 4 8
5 10 4 9 3 8 2 7 1 6 5 10 3 8 1 6 11 4 9 2 7
6 1 7 2 8 3 9 4 10 5 6 0 6 0 6 0 6 0 6 0 6
7 3 10 6 2 9 5 1 8 4 7 2 9 4 11 6 1 8 3 10 5
8 5 2 10 7 4 1 9 6 3 8 4 0 8 4 0 8 4 0 8 4
9 7 5 3 1 10 8 6 4 2 9 6 3 0 9 6 3 0 9 6 3
10 9 8 7 6 5 4 3 2 1 10 8 6 4 2 0 10 8 6 4 2
11 10 9 8 7 6 5 4 3 2 1
Self instances
Here we can select also (similarly as in G-systems) such numbers,
which are self, not nested.
(See above - rows and columns, which do not have number 0.) Tables
of self instances have φ(k) rows and columns, where φ is Euler
function.
T1 T2 x 1 T3 T4 T6 1 2 1 3 1 5 2 1 3 1 5 1
T5 T8 T10 T12
1 2 3 4 1 3 5 7 1 3 7 9 1 5 7 11
2 4 1 3 3 1 7 5 3 9 1 7 5 1 11 7
3 1 4 2 5 7 1 3 7 1 9 3 7 11 1 5
4 3 2 1 7 5 3 1 9 7 3 1 11 7 5 1
T7 T9 1 2 3 4 5 6 1 2 4 5 7 8 2 4 6 1 3 5 2 4 8 1 5 7 3 6 2 5 1 4 4 8 7 2 1 5 4 1 5 2 6 3 5 1 2 7 8 4 5 3 1 6 4 2 7 5 1 8 4 2 6 5 4 3 2 1 8 7 5 4 2 1
T11 1 2 3 4 5 6 7 8 9 10 2 4 6 8 10 1 3 5 7 9 3 6 9 1 4 7 10 2 5 8 4 8 1 5 9 2 6 10 3 7 5 10 4 9 3 8 2 7 1 6 6 1 7 2 8 3 9 4 10 5 7 3 10 6 2 9 5 1 8 4 8 5 2 10 7 4 1 9 6 3 9 7 5 3 1 10 8 6 4 2 10 9 8 7 6 5 4 3 2 1