Schematic algebra - Special cases
Cases of the R-systems
In the previous chapter we have passed general properties of R-systems, especially:
simple R-systems (r ε P) and composite R-systems (composite r)I this chapter and some next chapters we will concentrate on special cases.
In this chapter:
G-systems (r=nk−1) binary G-systems (r=nk−1, n=2) M-systems (r = (nk−1)/(n−1)) F-systems (r = nh+1) K-systems (r = (nk+1)/(n+1))--------
systems of complex numbers (u ε K) systems of algebraic numbers (u ε A) sign S-systems (+/− or 0)In the following chapters:
systems of power residues (k=κ(r,v)) systems of primitive roots (k=r−1) Legendre’s systems (k=κ(r,v) where u=v for u in the first row of the system) saturated systems (n=k) - Wieferich ’s systems (r=t²)G-Systems - An algebraic theory of musical structures
The area we are studying here is in the combinatorial theory known as Combinatorics of necklaces.
Instances
Let us think about arranging n elements into k cells. Let A be a set with n members (elements) with ordinal numbers given by the set E(A) = {0, 1, .., n-1}. Let B be a set with k members (cells) and ξ relation from E(B) to E(A).
000 001 010 100 011 110 101 111
ξ
(cells) E(B) ─────────────> E(A) (elements)
If numbers E(B) are positions of numbers (digits) from E(A), then written in n-number system we obtain nk possible numbers.
Let us mark the set of all these numbers I(n,k), members of this set are so called instances. Number n is called base and number k order of the set.
E.g. the sets A={p, q}, B={x, y, z} have their ordinal numbers given by E(A)={0, 1}, E(B)={0, 1, 2}.
Boole’s algebraValues of functions for logical sum (or) and logical product (and) of three variables can be arranged e.g. into the following schema (Y=yes,N=no):
Boole George| Boole George Irish mathematician, creator of the first algebra of mathematical logic. He was engaged also by quaternions and probability theory. His named get the used system of logic and -in computer terminology- also type of variables that can have just two values (True, False). |
Given values and or
────────────────────────
NNN N N
NNA NAN ANN N A
NAA AAN ANA N A
AAA A A
Classes of instances
Let relation G, defined as follows, be called G-relation.
ui (j) = nj ∙ gi (mod r), r = nk−1
Relation G is equivalence relation, so it will break-up instances ui (j) into classes I(n,k)/G.
Such a set of instances we name G-system and mark G(n,k). Because number r = nk−1, total number of instances is r+1 = nk,
where n is base and k is order of the G-system. Every class has its representative marked by gi., u(i,j) are instance numbers.
Every G(n,k) has m(n,k) classes marked g(i), i=1..m.
Instances of given class are called transpositions. System G(2,3) has 2³=8 instances I(2,3)={000, 001,.., 111} in m=4 classes. In this example (like in the example of Boole’s algebra), the instances are distinguished according to levels only, not according to classes.
Geometrical notionLet M be a set of 3 elements {A,B,C}.
Cube
000 {}
001 010 100 {A} {B} {C}
011 110 101 {A,B} {B,C} {A,C}
111 {A,B,C}
Instances of the system G(2,3) make subsets of the given set of M. Instances G(2,3) represent coordinates of apexes in 3 dimensional cube. Each instance of G(2,3) represents one apex, level instance evaluates distance of the coordinate origin.
In crystallography so called Miller’s indexes (h,k,l) are used.
System G(2,3) represents Miller’s indexes of the octahedron.

In the case of 12-tone system, there is n=2, k=12 and
structures make G(2,12). When A={exists, not-exists} and B={c, c#,
d, d#, e, f, f#, g, g#, a, a#, b},
then set of ordinal numbers E(A)={0,1}, E(B)={0, 1, .., 11}
and relation ξ makes a set I(2,12).
Diminished seventh chord (c,d#,f#,a) is class of
I(2,12) having 3 transpositions:
0/ 001001001001 [c, d#, f#, a]
1/ 010010010010 [c#, e, g, a#]
2/ 100100100100 [d, f, g#, h]
Particular instances of G-system arise as variations of class k from n elements, there is total nk variations.
Among instances all the possible permutation with repetition of selected elements are contained.
E.g. in G(3,5) there is 30 distinct instances with two zeros, two ones and one number two, i.e.. 00112, 01120, 11200, 12001,...
Number of such permutations with repetition is 5!/(2!2!1!) = 30 and because k=5 instance fill just 30/5 = 6 classes.
In binary systems, i.e. systems where n=2, is number of permutation with repetition equal to number of combinations.
E.g. in G(2,5):
1∙
00000
5!/5!0! = 1 =
![]()
5∙
00001
5!/4!1! = 5 =
![]()
5∙ 00011 + 5∙ 00101 5!/3!2!
=10 =
![]()
5∙ 00111 + 5∙ 01011 5!/2!3!
=10 =
![]()
5∙
01111
5!/1!4! = 5 =
![]()
1∙
11111
5!/0!5! = 1 =
![]()
Types of schema
We will distinguish three types of schemas: basic, contrast
and symmetric schema:
Basic schema Contrast schema Symmetric schema ────────────── ──────────────── ───────────────── 0 15 0 1 2 4 8 14 13 11 7 1 2 4 −7 3 6 12 9 12 9 3 6 3 6 −3 −6 5 10 10 5 5 −5 7 14 13 11 8 1 2 4 7 −1 −2 −4 15 0 0
In some cases, some schema is more convenient then the others.
DeformationFor r=15 field Z15 is projection (homomorfism) of field Z.
Integer Set of instances and classes
────────────────────────────────────────
0 0
1 2 4 8 1
Z ────> 3 6 12 9 ────> 3
5 10 5
7 14 13 11 7
15 15
Elements of the field Z15 makes e.g. the instances of G-system G(2,4).
Numbers of classes in G(2,4) are certain deformations (morfismus) of instance numbers.
Level of class
Sum of numbers (digits) from instances of a given class g in G(n,k) we call level L(g).
E.g. in systems G(2,k) is level given by number of ones in any of its instances.
In our case classes of G(2,4) have the following levels:
i/ Druh gi Binary schemas Level L(gi) ──────────────────────────────────────────────── 1/ 0 0000 0 2/ 1 0001 0010 0100 1000 1 3/ 3 0011 0110 1100 1001 2 4/ 5 0101 1010 2 5/ 7 0111 1110 1101 1011 3 6/ 15 1111 4
Generation of schemas of instances
Algorithm for list of numbers of representative classes in G-system is similar to Eratosthenes sieve (see Divisibility of numbers).
In our case we need to select numbers of representative classes from numbers of all instances.
Transpositions of instances in G-systems are analogous to prime multiples in Eratosthenes sieve.
E.g. G(2,4) has base n=2, order k=4 and module r =
nk−1 = 24−1=15.
We will cross out numbers g∙nj (mod r), j=1,2,...,
always with the smallest unused number g.
We will be interested in crossed numbers, we will write them into the schemas (on the right).
In this way we will step by step cross out all the given numbers (this is a next difference from Eratosthenes' sieve).
Given numbers: 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15
Used numbers Selected (crossed out) numbers
I/ 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 0
II/ 3,5,6,7,9,10,11,12,13,14,15 1 2 4 8
III/ 5,7,10,11,13,14,15 3 6 12 9
IV/ 7,11,13,14,15 5 10
V/ 15 7 14 13 11
15
Algorithm
Let us mark the set of all crossed numbers X. The
following block diagram describes algorithm for generation of
G-systems:
empty set X
↓
+--+- for g=0 to (n(k-1)-1) -- write the last class g=nk-1
| | |
| ↑ is class g in X ?
| | |
| +- YES-----+
| |NO
| |
| write g to X
| ↓
| assign u <- g
| |
|+---> while not u in X ----+
|| | |
|| write u to X |
|| | |
|| transpose instance |
|| u <- n * u |
|+------<-----+ |
+-------------<-------------+
This algorithm has the following disadvantage for large
systems. E.g. 2 MB (megabytes) of memory space are needed
for registration of crossed numbers of system G(2,24) (1
cross=1 bit, 1 byte = 2³ bits, 1 megabyte=220
byte).
Let us define g-number of a class as minimum of all instance
numbers (all transpositions) of the given class:
g = min(u0,u1,u2,..,uk−1) = min(u, u∙n mod r,
u∙n² mod r,...u∙nk−1 mod r)
For any number u we can determine number g - thereof algorithm:
│
┌───> for u=0 to (nk−1−1) ──> write the
last class g=nk−1
│
│
│ determine g <− min(u,u∙n mod r,...)
│
│
│ is g = u ──> write instance of class g
│
│
└──────<──────┴──────<──────┼
The second algorithm is time-consuming. To speed it up, some heuristics are needed - e.g. in case of binary systems g−number of class cannot be even,….
Examples of the output:
G(n,1)
G(2,1) G(3,1) G(4,1)
0 0 0
1 1 1
2 2
3
G(2,2) G(3,2) G(4,2)
0 0 0 6 9
1 2 1 3 1 4 7 13
3 2 6 2 8 10
4 3 12 11 14
5 7 5 15
8
G(2,3) G(3,3) G(4,3)
0 0 0 21
1 2 4 1 3 9 1 4 16 22 25 37
3 6 5 2 6 18 2 8 32 23 29 53
7 4 12 10 3 12 48 26 41 38
5 15 19 5 20 17 27 45 54
7 21 11 6 24 33 30 57 39
8 24 20 7 28 49 31 61 55
13 9 36 18 42
14 16 22 10 40 34 43 46 58
17 25 23 11 44 50 47 62 59
26 13 52 19 63
14 56 35
15 60 51
Program for listing of classes
Hint of program for the G-system G(n,k) (n=this.Degree, k=this.Order):
var r = (decimal)Math.Pow(this.Degree, this.Order) - 1;
this.Marked = new BitArray(r + 1, false);
var g = 1;
while (g ≤ r) {
if (g < this.Marked.Count && !this.Marked.Get(g)) {
this.AddStructure(g);
this.MarkInstancesOfClass(g, r, marked);
}
g = g + 1;
}
void MarkInstancesOfClass(int g, int r) {
var u = g;
while (u ≥ 0 && u < r && u < this.Marked.Count && !his.Marked.Get(u)) {
if (u < this.Marked.Count) {
this.Marked.Set(u, true);
}
u *= this.Degree;
while (u > r) {
u -= r;
}
}
}
Hint of program for the binary G-system G(n,k) (n=this.Degree=2, k=this.Order):
var r = (decimal)Math.Pow(this.Degree, this.Order - 1) - 1;
long num;
for (num = 1; num ≤ r; num += 2) {
decimal classNumber = this.DetermineClassNumber(this.Order, num);
if (num == classNumber) {
this.AddStructure(num);
}
}
num = (long)Math.Pow(this.GSystem.Degree, this.GSystem.Order) - 1;
this.AddStructure(num);
long DetermineClassNumber(byte order, long number) {
var minNum = number;
for (byte n = 1; n < order; n++) {
number = this.TransposeLeft(order, number);
if (number < minNum) {
minNum = number;
}
}
return minNum;
}
long TransposeLeft(int order, long number) {
var shift = (byte)(order - 1);
return (number & 1) << shift | number >> 1;
}
Rules of divisibility
Instance number ui (j) is relative prime with r=(nk−1), just if corresponding class number gi is relative prime to r.
Number of all relative primes with r is φ(r), where φ is Euler’s function.
If gi is relative prime with r, then its class must be self (not nested) class and such class has k instances. Proto k | φ(nk−1), i.e.:
φ(nk−1) mod k = 0
G(2,4)
0
* 1 2 4 8
3 6 12 9
5 10
* 7 14 13 11
15
In G(2,4) we have instance: (1, 2, 4, 8) a (7, 14, 13, 11) relative prime to 24 −1=15,
i.e. rows marked by asterisk. Because φ(24−1)=φ(15)=8, it holds φ(nk−1) mod k=8 mod 4=0.
Let us call the classes g, (g,r)=1, Euler’s classes, or shortly E-classes. These have E=φ(r) instances in e=E/k = φ(r)/k classes.
Coefficient g(n,k) = φ(nk−1)/k
n \ k │ 1 2 3 4 5 6 7 8 9 10
──────┼─────────────────────────────────────────────────
1 │ − − − − − − − − − −
2 │ 1 1 2 2 6 6 18 16 48 60
3 │ 1 2 4 8 22 48 156 320 1008
4 │ 1 4 12 32 120 288 1512 4096
5 │ 2 4 20 48 280 720 5580
6 │ 4 12 56 216 1240
7 │ 2 8 36 160
8 │ 6 18 144
9 │ 4 16 96
10 │ 6 30
n \ k │ 11 12 13 14 15 16 17 18 19
──────┼────────────────────────────────────────────┼
2 │ 176 144 630 756 1800 2048 7710 7776 27594
Assumption: for even k (n>2), k | g(n,k).
Let us order instances according to the following rule: any of two adjacent instances have to be different only in one element (digit) [Vrba],
for G(2,4) we get:
Binary numbers Decimal numbers
─────────────────────────────────────────────────────────────────
0000,0001,0011,0010,0110,0111,0101,0100 0, 1, 3, 2, 6, 7,5,4
1100,1101,1111,1110,1010,1011,1001,1000; 12,13,15,14,10,11,9,8
Numbers at odd positions corresponds to numbers relative
prime with module 15:
Odd positions:1,2,7,4,13,14,11,8
Even positions:0,3,6,5,12,15,10,9
G-systems are based on relation G, made by congruence according to module nk−1., where n is base and k order of the G-system.
Relation G is equivalence on set of all instances U. Class of equivalence G is set of all instances of the given class.
Factor set U/G is set of all classes (equivalence classes), i.e. break-up of set U to particular sets of instances according to classes.
Every instance u ε U, belong just to one class g(u). Assignment of an instance to some class pG: G−> U/G is called projection.
M-systems
 Let us
assume systems R(n,k,r), where:
Let us
assume systems R(n,k,r), where:
r = (nk−1)/(n−1)
We will call these systems Mersenne’s (M-) systems and mark
them M(n,k). System M(n,k) has r+1 instances {0,..,r}.
For n=2 M-systems melt with G-systems, because divisor (n−1)=1. So systems M(2,k) have r+1 = (2k−1)/(2−1)+1 = 2k instances.
Algorithm for M-systems
Algorithm for generation of M-systems is the same as algorithm for G-systems (see Algorithm for G-systems)
it uses different value r only.
Examples of output
M(2,1) M(3,1) M(4,1)
0 0 0
1 1 1
M(2,2) M(3,2) M(4,2)
0 0 0
1 2 1 3 1 4
3 2 2 3
4 5
M(2,3) M(3,3) M(4,3)
0 0 0
1 2 4 1 3 9 1 4 16
3 6 5 2 6 5 2 8 11
7 4 12 10 3 12 6
7 8 11 5 20 17
13 7
9 15 18
10 19 13
14
21
If kεP then M-system has (nk−n)/(n−1) self classes and therefore k | (nk−n)/(n−1) − because is in this case (n−1,k)=1,
we realize no more, than Fermat’s little theorem says.
Numbers relative prime with r always belong to subset of self instances, corresponding classes have always k transpositions.
It holds: k | φ(r) i.e. k | φ((nk−1)/(n−1))
It follows from the property of G-systems
k\φ(nk−1) and from the Fermat’s little theorem
k\(nk−n) for kεP, (k,n)= 1:
(nk−n)−φ(nk−1)≡0 (mod
k) i.e.
(nk−1+1−n)−φ(nk−1)≡0 (mod k)
Let use mark the expression nk−1−φ(nk−1) by ψ(nk−1) (see Euler’s function φ). So, it holds:
Ψ(nk−1) ≡ n−1 (mod k)
Count of numbers divisible with nk−1 belongs to the same class (mod k) as number n−1.
E.g.:
ψ(5³−1) ≡ 124 ≡ 1 (mod 3) (5−1)≡ 1
(mod 3)
ψ(27−1) ≡ 127 ≡ 1 (mod 7) (2−1)≡ 1
(mod 7)
Lucas-Lehmerova numbers
Lucas, Edouard A.| Lucas, Edouard A., 1842-1891, French mathematician. He studied number theory, especially Fibonacci sequences. He showed that the 2127 -1 is prime. |
Numbers Lk, defined by recurrent rule: L2=4, Lk+1=Lk² − 2 are called Lucas-Lehmer’s numbers.
Lehmer, Derrick Henry| Lehmer, Derrick Henry , 1905-1991, American mathematician. He was interested in testing of primality, in Lucas's functions, Bernoulli numbers, numerical analysis theory, in computers ... He introduced a new method of decomposition of numbers to a multiple of primes using the quadratic residues. |
k Lk Mk Lk/Mk ──────────────────────── 1 − 1 − 2 4 3 − 3 14 7 2 4 194 15 − 5 37634 31 1214 6 1416317954 63 −
To find if Mersenne’s number r=Mk=2k−1
is prime or not, so called Lucas-Lehmer’s test(for odd k) is
used:
number Mk is prime if it divides Lk.
Trivial subsystems
Let d be the smallest divisor d\M(n,k), that d ≡ 1 (mod k). Then R(n,k,r) for r=M(n,k)/d makes trivial subsystem M(n,k).
E.g. for n=2:
R(2,2,2): 0 R(2,3,7): 0 R(2,4,5): 0
1 2 1 2 4 1 2 4 3
3 3 6 5 5
7
Numbers r=M(n,k)/d takes for given n,k the following values:
n\k│ 2 3 4 5 6 7 8 ───┼───────────────────────── 2 │ 3 7 5 31 7 127 17 3 │ 1 13 5 121 ... 4 │ 5 7 17 ... 5 │ 3 31 .. 6 │ 7 43 .. 7 │ 3 19 .. 8 │ 9 ...
R(7,3,19):
0
1 7 11
2 14 3
4 9 6
5 16 17
8 18 12
10 13 15
19
R(4,4,17):
0
1 4 16 13
2 8 15 9
3 12 14 5
6 7 11 10
17
F-systems
Let us assume systems R(n,k,r), where:
r = nh+1
for hεN.
These systems we will call Fermat’s (F-) systems a mark F(n,h). System F(n,h) has r+1 instances {0,..,r}.
Algorithm for F-systems
Algorithm for generation of F-systems is again the same as algorithms for G-systems or M-systems)
it uses different value r only.
Examples of the output
F(2,1) F(3,1) F(4,1)
0 0 0
1 2 1 3 1 4
3 2 2 3
4 5
F(2,2) F(3,2) F(4,2)
0 0 0
1 2 4 3 1 3 9 7 1 4 16 13
5 2 6 8 4 2 8 15 9
5 3 12 14 5
10 6 7 11 10
17
F(2,3) F(3,3) F(4,3)
0 0 ....
1 2 4 8 7 5 1 3 9 27 25 19
3 6 2 6 18 26 22 10
9 4 12 8 24 16 20
5 15 17 23 13 11
7 21
14
28
Odd and even systems
0
1 4 3 12 9 10
2 8 6 11 5 7
13
Systems with odd and even number h are distinct. It holds (n+1)|(nh+1) for odd h, so odd systems can be divided by (n+1).
In a similar sense we have used division by (n−1) in M-systems.
E.g. v F'(4,3) is r=(4³+1)/(4+1) = 65/5 = 13, see Kummer’s K-systems.
Rules of divisibility
Because in F-systems is number of transpositions of each
self- class equal to 2k, in systems F(2, 2t) is equal to
2∙2t = 2t+1.
Euler has proved formula that was supposedly known to
P.Fermat:
d≡1 (mod 2t+1), for t≥ 0
With its help (for t=5) Euler has found decomposition of
number 4294967297.
For t=0,1,2 have systems F(2, 2t) this structure:
F(2,1) F(2,2) F(2,4)
0 0 0
1 2 1 2 4 3 1 2 4 8 16 15 13 9
3 5 3 6 12 7 14 11 5 10
17
Euler’s formula say that each divisor of numbers r=2(2t)+1 must be of the form s∙2t+1 + 1.
So every divisor must be made as number of instances in s rows plus one.
Starting with t=2 classes can make pairs.
E.Lucas has notes, that number s in the form s∙2t+1 + 1 must be (for t≥2) even. Let dεP, d>2 is some divisor of number F(2,2t).
So called Lucas' rule holds:
d≡1 (mod 2t+2), for t≥ 2
Every integer divisor of number F(2,2t) have form s∙2t+2 + 1 (sεN).
| Goldbach, Christian Russian mathematician. He focused primarily on the theory of numbers. Furthermore he studied endless series, theory of curves and theory of equations. |
Goldbach’s theorem
Each two distinct numbers of the form F(2,2t) are
relative primes, i.e. they does not have a common divisor:
(F(2,2t),F(2,2u)) = 1
In addition to this, F(2,2t) are also
relative prime with t, i.e.:
(t, F(2,2t)) = 1
Others
Numbers F(n,2t−2) have always residue 2 according
to module 2t, i.e. it holds F(n,2t−2) ≡ 2 mod
2t.
E.g. F(3,4)=82 ≡ 2 mod 16, F(3,8)=6562 ≡ 2 mod 32, ...
If F(2,2t)εP then it is a divisor of number F(3,22t−1).
 K-systems
K-systems
Let us assume systems R(n,k,r), where:
r = (nh+1)/(n+1)
these systems we will call Kummer’s (K-) systems and mark K(n,h).
Usually (for h<r) K-systems have order k=2h and correspond to systems R(n,2h,r).
Exception makes system K(2,3) with order k=2(h=r).
Into systems of prime r are just two classes nested, into systems with composite r more classes.
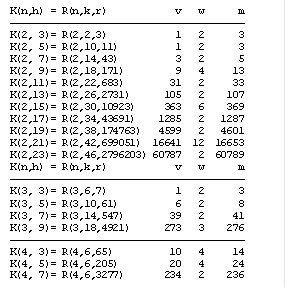
E.g. into K(4,3)= R(4,6,65) the system R(4,2,5) is nested:
n= 4 k= 6 r= 65 n= 4 k= 2 r= 5
0 0
1 4 16 64 61 49 1 4
2 8 32 63 57 33 2 3
3 12 48 62 53 17 5
5 20 15 60 45 50
6 24 31 59 41 34
7 28 47 58 37 18
9 36 14 56 29 51
10 40 30 55 25 35
11 44 46 54 21 19
13 52
22 23 27 43 42 38
26 39
65
C-systems
Let us consider systems R(n,k,r), where both numbers n or r can be complex. Generally we will speak about systems of complex numbers, C-systems.
Systems with complex module
Systems with prime module R=a+bi have the same structure as systems with module r, which is norm of the numbers R, i.e. r=a²+b².
In case r=1+i it holds i≡2 mod (1+i):
R(1,1,1+i) R(1,1,2) │ R(i,2,1+i) R(2,2,3)
0 0 │ 0 0
1 1 │ 1 i 1 2
i 2 │ 1+i 3
1+i 3 │
In case r=2+i is similarly i≡3 mod (2+i):
R(1,1,2+i) R(1,1,5) │ R(2,4,2+i) R(2,4,5)
0 0 │ 0 0
1 1 │ 1 2 1+i i 1 2 4 3
2 2 │ 2+i 5
i 3 │
1+i 4 │ R(i,4,2+i) R(3,4,5)
2+i 5 │ 0 0
│ 1 i 1+i 2 1 3 4 2
R(1+i,2,2+i) R(4,2,5) │ 2+i 5
0 0
1 1+i 1 4
2 i 2 3
2+i 5
System R(i,2,1+i) resp. R(2,2,3)=G(2,2) depicts structure of complex numbers.
There is zero element in the first row, real and imaginary
unit in the second row and smallest complex prime 1+I in the third
row:
00 0i+0 0 01 10 0i+1 1i+0 1 i 11 1i+1 1+ i
Quadratic systems
In two rows systems there must be 1 and also −1 always
in the first row, because both 1 and −1 are complex
powers i.e. quadratic residua.
R(1+i,2,2+i) R(4,2,5) 0 0 0 1 1+i 1 4 1 −1 2 i 2 3 −i i 2+i 5 0
Complex-conjugated systems
Two systems R(n1,k,r), R(n2,k,r) are complex-conjugated, if
their bases n1 and n2 are complex-conjugated.
For example systems R(1+i,3,3+2i) and R(1−i,3,3+2i):
R(1+i,3,3+2i) R(9,3,13) R(1−i,3,3+2i) 0 0 0 1 1+i 2i 1 9 3 1 1−i −2i 2 −i 1−i 2 5 6 2 i 1+i −1−i −2i −1 4 10 12 −1+i 2i −1 −1+i −2 +i 7 11 8 −1−i −2 −i 3+2i 13 3+2i R(9,3,13): 0 1 2 3 4 5 6 7 8 9 10 11 12 13 R(1+i,3,3+2i): 0 1 2 2i −1−i −i 1−i −1+i +i 1+i −2i −2 −1 3+2i R(1−i,3,3+2i): 0 1 2 −2i −1+i +i 1+i −1−i −i 1−i 2i −2 −1 3+2i
Complex units
Each self-row of the system R(1+i,3,3+2i) has one of complex
units {1,−i,−1,+i}.
R(1+i,3,3+2i) 0 1 1+i 2i +1 ≡ 1 2 −i 1−i −i ≡ 5 −1−i −2i −1 −1 ≡ 12 −1+i −2 +i +i ≡ 8 3+2i
These units correspond to numbers 1,5,12,8 in the system
R(9,3,13), i.e. to numbers of the first row of the system
R(5,4,13).
Because 5 ≡ −i (3+2i), we find complex units in the first row
of the system R(−i,4,3+2i):
R(5,4,13) R(−i,4,3+2i) 0 0 1 5 12 8 1 −i −1 +i 2 10 11 3 2 −2i −2 2i 4 7 9 6 −1−i −1+i 1+i 1−i 13 13
In the second row there are smallest complex even numbers and on the third row smallest complex half-even numbers.
Modules of G-systems
In case nεN is module of G-systems the number r=nk−1. For complex number N=a+bi a similar computation of the module does not hold.
(At least not in the sense of analogy to system with base n=a²+b²).
E.g. let n=5, k=3, r= 5³−1 = 124. Then according to it R= (2+i)³−1 = (2+11i)−1 = 1+11i. But norm of the expression 1+11i is number 122!?
S-systems
Sign systems
Number of classes in S(k) is equal to number of classes in G(2,k) minus number of distinct contrast classes (i.e. excluding inner contrast classes).
It holds:
ui (j) = nj ∙ gi or ui (j) = nj ∙ (r−gi) (mod r)
Let level of instance is absolute value of the sum of positive and negative units, e.g. −−−++ has level |−1−1−1+1+1| = 1.
Neutral class is class with zero level.
Outline of instances of systems S(k)
Classes Z(k): Instances Classes
Level g−numbers classes transp. total v w m neutr.
──────────────────────────────────────────────────────────
k=1:
− 1 0,1 2 1 2
2 1 0 1 0
──────────────────────────────────────────────────────────
k=2:
−− 2 0,3 2 1 2
−+ 0 1,2 1 2 2
2² 1 1 2 1
──────────────────────────────────────────────────────────
k=3:
−−− 3 0,7 2 1 2
−−+ 1 1,3 2 3 6
2³ 1 1 2 0
──────────────────────────────────────────────────────────
k=4:
−−−− 4 0,15 2 1 2
−−−+ 2 1,7 2 4 8
−−++ 0 3 1 4 4
−+−+ 0 5 1 2 2
24 2 2 4 2
Sign systems including zero
Outline of instances of systems S0(k)
System Level Instances Total
─────────────────────────────────────────────────────────
k=1: ( 2 classes )
0 0 1
− + 0 2
31
─────────────────────────────────────────────────────────
k=2: ( 4 classes )
00 0 1 *
−+ +− 0 2
0− 0+ −0 +0 1 4
−− ++ 2 2 *
3²
─────────────────────────────────────────────────────────
k=3: ( 6 classes )
000 0 1 *
0−+ −0+ +0− 0+− +−0 −+0 0 6
00− 00+ 0−0 0+0 −00 +00 1 6
−++ +−− +−+ −+− ++− −−+ 1 6
0−− 0++ −0− +0+ −−0 ++0 2 6
+++ −−− 3 2 *
3³
Systems of power residues
Let systems of power residues are the systems R(n,k,r), where
k=κ(r,v) = r div v
for v>1.
Specially in case v=2 we will speak about quadratic systems
(systems of quadratic residues),
resp. in case v=3 about cubic systems, and so on.
Quadratic residues
All numbers a² mod r are so called quadratic residues (residues with exponent m=2) according to module r. Others numbers (mod r) are so called quadratic nonresidues.
One of quadratic residues is always zero. All other quadratic residues and nonresidues for aε(1,r−1), rεP, arise symmetrically, i.e. exists r div 2 residues and r div 2 nonresidues.
Quadratic residues for r=13:
a² 1 4 9 16 25 36 49 64 81 100 121 144 a² mod 13 1 4 9 3 12 10 10 12 3 9 4 1
While looking for quadratic residues, it is not necessary to compute squares (second powers).
0 1 4 3 12 9 10 2 8 6 11 5 7 13
Quadratic residues (mod 13) are concentrated in the first row of the system R(4,6,13), quadratic nonresidues in the second row.
Median
Value r div 2 is used often used in theory of numbers. It appears in various formulas and so it exhort for a name.
We will call it median and mark it κ(r). Generally median of order s means number κ(k,s)=k div s, k,sεN.
For order 2 we will mark it simply (like second square root): κ(k)= κ(k,2)= k div 2.
Product residues a nonresidues
Quadratic residues a nonresidues according to rεP cover all numbers 1,2,..r−1 and make multiplicative groups Zr of order r.
│ residues │ nonresidues
│ 1 2 4 │ 3 5 6
───┼──────────┼─────────
1 │ 1 2 4 │ 3 5 6
2 │ 2 4 1 │ 6 3 5
4 │ 4 1 2 │ 5 6 3
───┼──────────┼─────────
3 │ 3 6 5 │ 2 1 4
5 │ 5 3 6 │ 1 4 2
6 │ 6 5 3 │ 4 2 1
Number 1 appears in the table only as product of residue* residue or nonresidue* nonresidue.
If n, n' are dual bases, it holds p\(n∙n'−1), i.e. n∙n' ≡ 1 (mod p).
Therefore, when n is quadratic residue (mod p), is n' also quadratic residue.
Quadratic residues are in the top left quadrant of the table:
Groups of quadratic residues
Quadratic residues make for rεP subgroups Kr(∙) group Zr(∙).
Order of these subgroups is median κ(r).
K3 K5 K7 K11 K13
1 1 4 1 2 4 1 3 4 5 9 1 3 4 9 10 12
4 1 2 4 1 3 9 1 4 5 3 9 12 1 4 10
4 1 2 4 1 5 9 3 4 12 3 10 1 9
5 4 9 3 1 9 1 10 3 12 4
9 5 3 1 4 10 4 1 12 9 3
12 10 9 4 3 1
| Carmichael, Robert Daniel |
Carmichael‘s theorem
R.D.Carmichael (1905) reformulated Wilson’s theorem. Number r is prime, if it holds:
(κ(r)!)² + (−1)κ(r) ≡ 0 mod r
Wilson‘s theorem
Wilson’s theorem can be rewritten into form:
(−1)κ(r)∙(κ(r)!)² ≡ −1 (mod r)
Sylvester, James Joseph| Sylvester, James Joseph [], 1814-1897, English mathematician, a leading creator of a new symbolism. He was interested in the theory of elementary divisors, algebra forms, theory of determinants. Along with Cayley he created the first algebraic theory of invariants of quadratic forms. He was also concerned in mechanics. |
Sylvester‘s theorem
Sylvester (1860)
∑κ(r,k)∙φ(k) = n∙(n+1)/2
For r=5:
k=1 5∙φ(1) = 5
k=2 2∙φ(2) = 2
k=3 1∙φ(3) = 2 5∙6/2 = 15
k=4 1∙φ(4) = 2
k=5 1∙φ(5) = 4
───────
15
Euler’s criterion
Let us write for uεN, rεP:
Q(u,r) = uκ(r) mod r
If r|u then it holds:
Q(u,r)= 0
E.g. Q(14,7) = 14³ mod 7 = 0.
It holds for quadratic residues:
Q(u,r)= 1
────────────────────────────
16 mod 13 = 1 mod 13 =1
46 mod 13 = 4096 mod 13 =1
36 mod 13 = 729 mod 13 =1
126 mod 13 =2985984 mod 13 =1
96 mod 13 = 531441 mod 13 =1
106 mod 13 =1000000 mod 13 =1
|
It holds for quadratic nonresidues:
Q(u,r)= −1
─────────────────────────────
26 mod 13 = 64 mod 13 =−1
86 mod 13 = 262144 mod 13 =−1
66 mod 13 = 46656 mod 13 =−1
116 mod 13 =1771561 mod 13 =−1
56 mod 13 = 531441 mod 13 =−1
76
|
Number u is quadratic residue or nonresidue according to value Q(u,r)=uκ(r) mod r.
It is so called Euler’s criterion.
When Q(u,r)= 1 (resp.−1), is number u quadratic residue (resp. nonresidue) according to module r.
Euler’s criterion is abstract and simple. It is advantageous particularly for smaller numbers r.
Emergence of Euler‘s criterion
Number u is quadratic residue, if it exists such number a, that it holds:
a² ≡ u (mod r).
After powering of this formula to exponent κ(r)=(r−1)/2 we
get:
a2(r−1)/2 ≡ ar−1 ≡ uκ(r) (mod r)
E.g. for r=17, u=19, a=11 it holds 11² ≡ 19 (mod
17), so 19 is quadratic residue mod 17. After squaring to
κ(17)=8:
1116 ≡ 198 ≡ 1 (mod 17).
Euler’s criterion follows from Fermat’s little theorem. Because ar−1 ≡ 1 (mod r) then uκ(r) ≡ 1 (mod r) in case when u is quadratic residue.
In power systems R(n,k,r) it holds nk ≡ 1 mod r (see Geometric sequences). Number 1 is always in the first row, therefore for n=1 is nκ(r) ≡ 1 mod r.
Therefore in two rows systems there are numbers nκ(r) ≡ 1 mod r (i.e. quadratic residues) in the first row and numbers nκ(r) ≡ −1 mod r (i.e. quadratic nonresidues) in the second row.
Residues of higher degrees
Biquadratic residues
E.g. numbers u=a4 mod 13 for all aε(1,12):
a4 1 16 81 256 625 1296 2401 4096 6561 10000 14641 20736
a4 mod 13 1 3 3 9 1 9 9 1 9 3 3 1
Biquadratic residues appear in the first row of systems R(n,κ(r,4),r), e.g. R(5,4,13). Because a4 mod r=(a²)² mod r, biquadratic residue is also quadratic residue.
R(5,4,13): R(4,6,13):
0 0
1 3 9 1 4 3 12 9 10
2 6 5 2 8 6 11 5 7
4 12 10 13
7 8 11
13
Gauss‘s classes
In analyzes of biquadratic residues, Gauss divide numbers into 4 classes A,B,C,D according to following schema:
A │ 1 g4 g8 ... │ biquadratic residua
B │ g g5 g10 ... (mod r) │ nonresidua
C │ g² g6 ... │ quadratic residua
D │ g³ g7 ... │ nonresidua
where g is such number, that all numbers 1,g,...gr−1 are (mod r) are all distinct (see primitive roots of numbers r).
E.g. for r=17, g=3 (on the right with numbers in classes ordered according to values)
A 1 13 16 4 A 1 4 13 16
B 3 5 14 12 i.e. B 3 5 12 14
C 9 15 8 2 C 2 8 9 15
D 10 11 7 6 D 6 7 10 11
Distribution of numbers in classes corresponds to distribution of instances in R-system, in our case R(4,4,17):
R(4,4,17)
0
1 4 16 13 │ A (1)
2 8 15 9 │ C (g²=9)
3 12 14 5 │ B (g=3)
6 7 11 10 │ D (g³=27≡10)
17
Relation of classes
Result of product of any number of class C (e.g.9 mod 17) with number of class D (e.g.7 mod 17) belongs
to class B (9∙7=63≡12 mod 17). Generally the multiplication is directed by the following table:
│ A B C D Z4+│ 0 1 2 3
──┼───────────── ──┼────────────
A │ A B C D 0 │ 0 1 2 3
B │ B C D A 1 │ 1 2 3 0
C │ C D A B 2 │ 2 3 0 1
D │ D A B C 3 │ 3 0 1 2
This table corresponds to table of addition in field Z4 (see groups).
Complex units
In solution of problem of biquadratic residues Gauss have
used complex numbers. He assigned complex units 1,i,−1,−i to
classes A,B,C,D.
Let us mark A,B,C,D by numbers (characters) c=0,1,2,3 and numbers
(instances) in classes by letter u. It holds:
uκ(r,4) ≡ ic mod r
where i is imaginary number, i=√−1.
Centers of multiplicative tables
k=2: k= 3: k = 4: k = 5: k = 6:
1 1 2 1 2 3 1 2 3 4 1 2 3 4 5
2 1 2 0 2 2 4 1 3 2 4 0 2 4
3 2 1 3 1 4 2 3 0 3 0 3
4 3 2 1 4 2 0 4 2
5 4 3 2 1
In the centre of multiplicative tables (mod k) there is just one number (if k is even) or there are four numbers (if k is odd).
These four numbers contains numbers κ(k)² mod k and κ(k)∙(κ(k)+1) mod k.
For even k:
For k=4s (i.e. k is divisible by 4) is in the centre of the table zero. For k=4s−2 is in the centre number 2s−1.E.g. for k=6 (s=2) is in the centre number 3 (i.e. 2∙2−1).
For odd k:
For k=4s−1 are the four numbers build from s and 3s−1. For k=4s+1 similarly from s and 3s+1.| Numbers in the centers of multiplicative tables (mod k) does not depend on number k only, but also on its correspondence to 4 classes: 4s−1, 4s, 4s+1 and 4s+2. |
Odd number n is genuine if its median κ(n) is odd. Genuine odd numbers (p,q,...):
is not a square - second power has always form 4s or 4s+1 genuine odd primes (so called Gauss' primes) cannot be in complex field decomposed(e.g. 3,7,11,19,23,31,43,47,59,67,71,79,83,...)
congruence x²+y²≡0 (mod p) is not solvable (pεP) number aεN can be written as sum of two (relative prime) squares, if there is no genuine odd prime in its partitionNongenuine odd numbers (p,q,...) have the following properties:
make square, i.e.(2k+1)² has always form 4s+1 Euler has proved, that primes of form 4s+1 are always unique sum of two squares(e.g. 1=0+1, 5=1+4, 13=4+9, 17=1+16, 29=4+25, 37=1+36, 41= 16+25, 53= 4+49, 61=25+36, 73= 9+64, 89=25+64, 97= 16+81, 101= 1 +100) nongenuine odd primes can be in complex field decomposed (e.g. 5=(2+i)(2−i), 13=(3+2i)(3−2i),...) some of so called perfect numbers can be – according to Euler – expressed in form pq∙N², where p and q are nongenuine odd numbers. for r = 4s+1εP Carmichael’s theorem get form:
(κ(r)!)² = −1 mod r
Euler’s classes
Euler has proved some more sophisticated theorems about
classes (mod 4):
Let (a1,b1)=1, (a2,b2)=1 and numbers p1,p2 ε P. Let us mark f(a,b)
= a²+n∙b².
If p1 ≡ p2 (mod 4n) and p1 | f(a1,b1) then also p2 | f(a2,b2).
E.g.
for n=1: 5|(1+4),
13|(4+9) a 5 ≡ 13 (mod 4);
or 13|(1+25),
17|(9+25) a 13 ≡ 17 (mod 4).
for n=2: 11|(4+2∙9), 59|(9+2∙25) a 11 ≡ 59 (mod 8).
Residues of exponent v
Let us consider R-systems (rεP), that have exactly v self-rows. Self-row is row, that have just k instances (rows 0 and r are not self rows, they are nested).
Such systems have order k=r div v = κ(k,v).
In the first row are residues of exponent v, i.e. so called. v-tic residues (for v=2 quadratic residues, v=3, cubic residues,...).
In other rows there are nonresidues (of exponent v).
E.g. cubic residues, i.e. numbers u=a³ mod r are in the first row of schemas R(n,κ(r,3),r):
For r=7: For r=13:
a3 1 8 27 64 125 216 a3 1 8 27 64 125 216 343 512 729
a3 mod 7 1 1 6 1 6 6 a3 mod 13 1 8 1 12 8 8 5 5 1
R(6,2,7): 0 R(5,4,13): 0
1 6 1 5 12 8
2 5 2 10 11 3
3 4 4 7 9 6
7 13
Euler‘s generalized criterion
Systems with v self-rows, have order k=r div v =
κ(r,v), i.e. these are systems R(n,κ(r,v),r).
E.g. R(5,4,13) has 3 self-rows, i.e. v=3 and order k=13 div 3 =
4.
R(5,4,13):
0
1 5 12 8
2 10 11 3
4 7 9 6
13
Number u is v-tic residue, if exists such a, that it holds av ≡ u (mod r).
After powering to κ(r,v) we get:
av(r−1)/v ≡ ar−1 ≡
uκ(r) (mod r).
This is an analogy of formula in the previous paragraph.
Number u is v-tic residue, when Qv(u,r)= 1 where:
Qv(u,r) = uκ(r,v) mod r.
Legendre‘s systems
Number u is v-tic residue (mod r), if it is in the first row
of the system R(n,k,r), where k=κ(r,v) (see Euler’s generalized
criterion).
In case u=v, is number u is by itself u-tic residue. We call
Legendre’s systems the systems R(n,k,r), that have v
self-rows
and in the first row number v.
0 1 2 4 │ v = 2 3 6 5 │ 7 ── k=3 ──
E.g. R(2,3,7) is Legendre’s system: it has 2 self-rows
and in the first row number 2 (number 2 is quadratic residue mod 7).
It holds: 2³ ≡ 1 (mod 7).
Generally according to Euler’s criterion must be Qv(v,r) = vκ(r,v) mod r = 1, where exponent v is order of system: k=κ(r,v).
Therefore in Legendre’s systems R(n,κ(r,v),r) it holds:
vk ≡ 1 (mod r)
Legendre, Adrien-Marie| Legendre, Adrien-Marie. French mathematician and physicist. He greatly influenced next development of number theory: he discovered quadratic reciprocity law and generalized relations concerning large Fermat's theorem. He studied also ellipsoids, elliptic functions and integrals. He worked on meassuring of the Earth, derived new formulas for spherical triangles. He managed compilation of logarithmic and trigonometric tables. |
Value kk (mod r)
Because k=κ(r,v), we get k∙v = r−1 (rε P). So (r−1)k = (v∙k)k = kk∙vk, where:
vk ≡ 1 (mod r) (r−1)k ≡ (−1)k (mod r).After substitution we get:
kk ≡ (−1)k (mod r)
Systems with even order
When k is even (k=2t) tak (−1)k = 1 it holds:
v²t ≡ (2t)2t ≡ 1 (mod r)
Here r= 2tv+1, rε P.
E.g. for t=1,2,3,4 we get values:
t (2t)2t rozklad T=(2t)2t−1
────────────────────────────────────────────────
1 2² = 4 3
2 44= 256 255 = 3∙5∙17
3 66= 46656 46655 = 5∙7∙31∙43
4 88 = 16777216 16777215 = 3²∙5∙7∙13∙17∙241
Partition of numbers T helps to select numbers r.
We will derive one appropriate Legendre’s system with even order for each t:
t=1 r= 3, v= 1, k=2
0
1 2
3
t=2 r=17, v= 4, k=4
0
1 4 16 13
2 8 15 9
3 12 14 5
6 7 11 10
17
|
t=3 r=31, v= 5, k=6
0
1 6 5 30 25 26
2 12 10 29 19 21
3 18 15 28 13 16
4 24 20 27 7 11
8 17 9 23 14 22
31
t=4 r=17, v= 2, k=8
0
1 2 4 8 16 15 13 9
3 6 12 7 14 11 5 10
17
|
Systems of primitive roots
We will call systems of primitive roots the systems R(n,k,r), where:
k=r−1
Systems of primitive roots supply the case v=1 of systems of power residues.
Primitive roots
The powers of a given root can pass all other roots only in case, when s=h, i.e. when order (s) of given root is equal to exponent of binomial equation h.
The roots with this property we call primitive roots. Fundamental root α is always one of primitive roots.
Let us select such systems R(n,k,r) (for rεP) that have r−1 transpositions, i.e. that (excluding numbers 0 and r) does not break rows. For r=7 there exist 2 such systems, R(3,6,7) a R(5,6,7):
R(3,6,7): R(5,6,7):
0 0
1 3 2 6 4 5 1 5 4 6 2 3
7 7
Each of these systems has just one self-class with representative g=1. For α=n, j=0,..,r−1 expressions αj pass all instances
and makes so integer analogy of primitive roots of equation x6−1=0 with exponent h=r−1=6 (see cyclic groups,...)
Number of primitive roots is equal to number of primes relative to exponent h. Binomial equation xh−1 = 0 has therefore φ(h) primitive roots.
For given rεP exists always φ(r−1) systems with primitive root as a base n. E.g. for r=7 there exist φ(6)= 2 primitive roots.
Layout of primitive roots
The root xj(h) is primitive root of equation xh−1=0, when numbers j and h are relative prime, (j,h)=1.
E.g. for number h=6, the numbers j=1 and 5 points to primitive roots:
j: 0 1 2 3 4 5
────────────────────────────────────
R(3,6,7): 1 3 2 6 4 5
R(5,6,7): 1 5 4 6 2 3
For r=11 there exist φ(10)= 4 primitive roots and therefore four distinct systems with full number of transpositions:
R(2,10,11): R(6,10,11): 0 0 1 2 4 8 5 10 9 7 3 6 1 6 3 7 9 10 5 8 4 2 11 11 R(7,10,11): R(8,10,11): 0 0 1 7 5 2 3 10 4 6 9 8 1 8 9 6 4 10 3 2 5 7 11 11
Primitive roots 2,6,7,8 are at positions 1,3,7,9 (i.e. numbers relative prime with r−1=10).
0 1 2 3 4 5 6 7 8 9
───────────────────────────────────────────────────────
R(2,10,11): 1 2 4 8 5 10 9 7 3 6
R(6,10,11): 1 6 3 7 9 10 5 8 4 2
R(7,10,11): 1 7 5 2 3 10 4 6 9 8
R(8,10,11): 1 8 9 6 4 10 3 2 5 7
For r=13 φ(12)= 4 primitive roots exists: 2,6,7,11. These roots make bases of systems R(2,12,13), R(6,12,13), R(7,12,13) a R(11,12,13).
R(n,k,13) 0 n │ k +−> 1 2 4 8 3 6 12 11 9 5 10 7 R(2,12,13) ────┼──── │ 13 1 │ 1 │ 2 │ 12 ──┼ 0 3 │ 3 +−> 1 6 10 8 9 2 12 7 3 5 4 11 R(6,12,13) 4 │ 6 │ 13 5 │ 4 │ 6 │ 12 −+ 0 7 │ 12 ───> 1 7 10 5 9 11 12 6 3 8 4 2 R(7,12,13) 8 │ 4 13 9 │ 3 10 │ 6 0 11 │ 12 ───> 1 11 4 5 3 7 12 2 9 8 10 6 R(11,12,13) 12 │ 2 13
Criterion for primitive roots
Let r is odd prime (i.e. rεP, r>2).
According to Fermat’s little theorem is nr−1 ≡ 1 mod r, i.e. r |(nr−1−1).
When r is odd, number r−1 is even and we can expand
expression nr−1−1 according to formula
a²−b² = (a−b)(a+b):
nr−1−1 = (nκ(r)
−1)(nκ(r) +1)
Difference of coefficients is 2, so the product cannot have divisor greater than 2.
Number r must be therefore a divisor of one of numbers (nκ(r) −1) or (nκ(r) +1).
If (nκ(r) −1) was the divisor then nκ(r) ≡ 1 mod r, but it is for primitive root impossible (system can not break row on the index κ(r)...)
For primitive root n (according to module r) it holds:
nκ(r) ≡ −1 mod r
So primitive roots keep the same relation as quadratic nonresidues (see Euler’s criterion).
Not all quadratic nonresidues are primitive roots, primitive roots make subset of quadratic nonresidues.
Monocycles
Sequence of numbers B1,B2,....Bn,A1,A2,..An can be reordered to sequence A1,B1,A2,B2,... with help of one permutation.
We are looking for permutation with just one cycle (problem "perfect shuffle" in the theory of sort algorithms).
Let use consider an equivalent problem:
Sequence of 2n numbers 0,1,..,2n−1 have to be reordered by one permutation, that n odd numbers come in front of n even numbers.
We are interested for which n can be such reordering made by permutation with just one cycle (monocycle).
Monocycle exists only when number 2 is primitive root according to module p=2n+1.
Example of a monocycle
For n=5 (p=11) has permutation just one cycle [0 1 3 7 4 9 8 6 2 5]:
j 0 1 2 3 4 5 6 7 8 9
i 1 3 5 7 9 0 2 4 6 8
Origin of cycle:
j 0 1 2 3 4 5 6 7 8 9 2j−1 0 1 3 7 15 31 63 127 255 511 (2j−1) mod 11 0 1 3 7 4 9 8 6 2 5
Cycle has full length because there does not exists j<p−1, that (2j−1) mod p=0.
Example of more cycles
For n=3 (p=7) is permutation composed of two cycles [0 1 3][2 5 4]:
Permutation: Vznik cyklu:
j 0 1 2 3 4 5 j 0 1 2 3 4 5
i 1 3 5 0 2 4 2j−1 0 1 3 7 15 31
(2j−1) mod 7 0 1 3 0 1 3
Permutation does not make monocycle: cycle has not full length, because (2³−1) mod 7 = 0.
Briggs Rafael| Briggs Rafael, 1526-1572, English mathematician, published the first table of decimal logarithms. |
Logarithmic function
Special meaning in math has (for P=ap, Q=aq, a,p,q,P,Q,r ε R)
exponential function, that convert additional operation to multiplication:PQ = ap aq = ap+q
e.g. 5∙125=51 5³ = 51+3= 54 = 625, and
Neper(Napier) John| Neper(Napier) John Scottish mathematician, inventor of the natural logarithms. Dealt with spherical trigonometry and calculation methods. |
logarithmic function , that convert multiplicative operation to addition
logaPQ =logaP+logaQ = p+q
Repeated addition of logarithms ( multiplying the logarithm by a number ... ):logaPv = v logaP = vp
e.g. log5625 = log554 = 4∙ log55 = 4.
As bases are used:
In decimal system base a=10 (decimal logarithms…) Music tones in ratio 2:1 (octave) are similar. In this case binary logarithms (base a=2) can be used.(We find these logarithms also e.g. in theory of information…)
In mathematic analysis Euler’s number e=(1+1/n)n is significant (higher n, more precise e).Euler’s number is base of natural logarithms a=e (or a=1/e how J.Napier originally defined).
In theory of numbers integer logarithms were introduced. Their bases are so called primitive roots.
Integer logarithms
Let us consider exponential function: y=nx mod r,
that assign numbers {1..r−1} to transpositions xε{0..r−2}.
Inverse function to this is an analogy of logarithmic function: x=
ind(y) mod (r−1).
If n is primitive root, the assignment is definite.
If module of exponential function is r then module of inverse function is (r−1).
E.g. for r=11, n=2:
x 0 1 2 3 4 5 6 7 8 9
y=nx mod r 1 2 4 8 5 10 9 7 3 6
y 1 2 3 4 5 6 7 8 9 10
x=ind(y) mod r−1 0 1 8 2 4 9 7 3 6 5
Some congruences can be solved like logarithmic
equations:
E.g. a³≡9 (mod 11):
a³ ≡ 9 (mod 11)
ind(a³) ≡ 3∙ind(a) ≡ ind(9) (mod 10)
ind(a) ≡ ind(9)/3 ≡ 6/3 ≡ 2(mod 10)
a ≡ 4 (mod 11) Zkouška: 4³ mod 11 = 64 mod 11 = 9
From criterion for primitive roots follows, that index
numbers −1 (mod r) is κ(r).
E.g. for r=11:
y
1 2 3 4 5 6 7 8 9 10
x=ind(y) mod (r−1) 0 1 8 2 4 9 7 3 6 5
ind(−1)= ind(r−1)= ind(10) = 5 κ(r)
= 11 div 2 = 5.
Product of primitive expressions
Among the R-systems with r=5 are φ(4)= 2 systems of primitive roots:
R(2,4,5) 0 R(3,4,5) 0
1 2 4 3 1 3 4 2
5 5
We will call primitive expressions r(x) the polynomials with
coefficients taken from instances of systems of primitive
roots.
r1(x)=
1+2x+4x²+3x³ r2(x)=
1+3x+4x²+2x³
We are interesting in the product of all such expressions for given r when xr−1=xk=1.
For r=5 is: r1(x)∙r2(x) = 5(6+5x+4x²+5x³).
If expression V(x) mod r can be substituted for V(x), then:
[r1(x)∙r2(x)]5 =
5(1−x²).
(Expression ∑s² for s=1,..,p−1 in products is always
divisible by p, because ∑s² =
(p−1)p(2p−1)/6,...).
For r=7:
r1(x)=
1+3x+2x²+6x³+4x4+5x
5
r2(x)=
1+5x+4x²+6x³+2x4+3x5
r1(x)∙r2(x) =
7(13+10x+11x²+8x³+11x4+10x5
and [r1(x)∙r2(x)]7 =
7(1−x³)(−1+3x−3x²).
These expressions, after substitution x=α, where α is complex root of equation xr=1, cohere with Kummer’s theory of cyclic numbers.
W-systems
We call Wieferich's (W) systems the systems R(n,k,r), where:
r = t²
and tεN. We are interested especially in the case n=2 with t odd prime (tεP).
We will try to observe, what properties the W-systems have in the case t is so called.Wieferich's prime.
W-systems - Examples of output
R(2, 20, 5²)
0
1 2 4 8 16 7 14 3 6 12 24 23 21 17 9 18 11 22 19 13
5 10 20 15
25
R(2, 21, 7²)
0
1 2 4 8 16 32 15 30 11 22 44 39 29 9 18 36 23 46 43 37 25
3 6 12 24 48 47 45 41 33 17 34 19 38 27 5 10 20 40 31 13 26
7 14 28
21 42 35
49
| Wieferich, Arthur [], 1884-1954, the German mathematician and teacher. He proved, that validity of the Last Fermat Theorem can - in the first case - distort at most only some of (so-called Wieferich's) primes. |
Wieferich's primes
Wieferich's prime is such p
, pεP,
that
:
2
p
-1
≡ 1 (mod
p
2
)
Only known Wieferich's primes are 1093 and 3511.
Orders of W-systems
Orders of W-systems are in the observed cases (t=3,5,7,..) larger than the value t, so k>t (eg. k=20 for t=5; k=21 for t=7; ...) .
Even, it holds t | k (in our example 5 | 20; 7 | 21). Order k ofted have value k = t(t-1), so k | t(t-1) (e.g. 20 | 5*4, 21 | 7*6).
In the system R(n,k,t²) the number W=2t-1 - 1 mod t² must lay in the first row. It determines the order of the system k, k | (t-1).
Here is the main distinction of systems R(n,k,t² ) of common prime t from systems with Wieferich's prime t.
In the first case k | t(t-1), but in the second case the order k must be necessarily less : k | (t-1) .¨
System R(2, 364, 1093²)
In the system of order k = 364 there are m=3284 classes, from these v=3282 are self classes and w=2 are nested classes (from the order 1).
Thus, in total system contains 3282*364 + 2* 1 = 1194650 instances (=1093²+1).
System R(2, 1755, 3511²)
In the system of order k =1755 there are m=7026 classes, from these v= 7024 are self classes and w=2 are nested classes (from the order 1).
Thus, in total system contains 7024*1755 + 2* 1 = 12327122 instances (=3511²+1).
Nesting in W-systems
Order of any system di nested into R(n,k,t² ) have to divide self order k, so di | k, while nesting is determined by common divisor 2d-1 and t² .
For prime tεP and (2d-1, t² )>1 is the only case t | 2d-1 for some di | k.
In R(2, 20, 5²) is k= 2²*5 and for d=5 it holds t | 25-1. In R(2, 20, 7²) is k=3*7 and for d=3 it holds: t | 2³-1.
Therefore these systems have nested classes with number k/t of transpositions.
In the case, where for all di | k holds (2d-1, t² )=1, the system has only self classes and trivial classes nested from order d=1.
Because number of trivial classes is always 2 and total number of instances is t²+1, the self classes cover t²-1 instances.
Each self instance has k transpositions, so k |
t²-1.
These relations hold also in both of the mentioned systems
-
in R(2, 364, 1093²)
364 |
1093²
-1
and in R(2, 1755, 3511²)
1755 |
3511²-1.
Little Fermat Theorem
In the systems R(n,k, t² ) is 2t-1 = a* t² + h (a,hεN), where h=1 in case of Wieferich's prime t.
In other cases we get - e.g. for t=5: h=16, for t=7: h=15, ... where it holds: h mod t = 1.
So h = b*t + 1 (bεN) and we get from the conjunction with the previous relation:
2t-1 = a* t² + b*t + 1
It is clear, that the whole equation is divisible by t only in case t | 2t-1 -1.
More general case
Equation 2t-1 = a* t² + b*t + 1 is satisfied in case b=0 by Wieferich's primes 1093 and 3511.
For the next values b = 1,2,... we get the folowing values t.
b=1: t=3,29,37,3373; b=2: t=7,71,379; b=3: t=13,19,173; b=5: t=11; b=6: t=31, 89; ...