Music theory - Energy
| Micka Josef , 1903-1993, Czech violinist, violin teacher and music theorist, professor of violin at the Academy of Performing Arts. In brief treatise on musical dynamics he indicated the most general (energy) principles that govern the perception of music tracks. He explained, where it is justified to gain (crescendo) and where to weaken (decrescendo) and attempted to reconstruct the dynamic ticks in music writings without labeling (Bach's fugues, ...). |
Each musical element needs a certain amount of energy to its realization: higher tones, quick and irregular rhythms, dissonant harmonies... consume more power and require more energy from its source.
Interactions of tones
Energy of harmonic oscillation is directly proportional to the amplitude and frequency. Therefore higher tones require higher energy than the lower. However, if all tones are produced (by an interpreter) with the same energy, then necessarily (according to Josef Micka) the lower tones (i.e.lower frequency) will sound with a higher amplitude, that is stronger.
Energy bands
Let the energy band is the carrier of energy pertaining to the frequency. Suppose that this energy does not vanish simultaneously at the moment the tone stops to sound and persists (in bands) in the psycho-acoustic form. Longer sounding tones supply into bands more energy than shorter tones. The cumulated energy remains in the bands until it is exhausted (pumped out) by external forces. We assume - By analogy with similar physical phenomena - these action of external forces:
Resistance of the environment: causes gradual loss of energy the bands..
Interaction between bands redistribute and consume energy of bands.
Time loss can be assumed e.g. in the form
E = E0 /exp(kt)
where t is time and k a constant (K.Asherov).
Janáček Leoš| Janáček Leoš , 1854-1928, Czech composer and music theorist. He was interested in folk art, developed his own characteristic style by using tune folk elements. In an effort to express his musical ideas as clearly as possible, he introduced a number of specific terms - after-feeling tone (pacitový tone), weave-point (spletna), time-root (sčasovka), .... |
The root band
The band, which is at any given time carrier of the largest energy, iss called root-band. We call the characteristic expressing the relative level of energy in the band by term rootness.
The tone of pitch v, loudness h and length d seems to deliver energy E to its band proportional to the relation:
E=d∙(h/v)
Rootness of the tone: depends largely on the structure of the chord.
Weave-point
So called weave-point (spletna in Czech) plays an important role in the Janáček's theory of harmonic connections. The weave-point is formed by relations between the chord that just expires - so called after-feeling (pacitový in Czech) - and the chord that just starts - i.e. just-feeling (pocitový in Czech). L.Janáček distinguished - depending on the weave-point type - three main types of harmonic connections: "connection of reconciliation" (semitone lead), "connection of exchange" (fifth relation).
Janeček Karel| Janeček Karel , 1903-1974, Czech music theorist and composer (creator of piano, chamber, vocal and orchestral music). One of the biggest Czech music theorists, systematic. Dealt with the theory of the composition and harmony of music, both classical and modern. Systematically listed all possible chords of 12-tone system and evaluate them by some characteristics (dissonance, symmetry,...) He devoted himself to music tectonics, musical forms, the science of the melody, analysis of music tracks, as well as compositional issues (imagination, talent, ...) He generalized the thoughts of his predecessors and formulated them more precisely. He documented all the principles by samples of musical works. |
Imaginary tones
Prof. Karel Janecek reformulated Janáček's considerations on the weave-point in the theory of imaginary tones (see Fundamentals of modern harmony []). Karel Janeček distinguishes harmonic and tonal imaginary tones, now we notice only the former. Harmonic imaginary tones "sound" after the completion of real tones. Harmonic imaginary tones - just as real tones and together with them - create a harmonic structures. Imaginary tones sound as long as they have enough energy. Each imaginary harmonic tone can be canceled by a real tone, wherein consonant intervals and tritonus cancels imaginary tones slowly, whole tones normally and semitones quickly. K.Janeček demonstrates the theory on several examples and clarifies certain laws of classical harmony. He also defines the principle of pure tonic using the theory of imaginary tones.
Types of interactions
It is irrelevant to compose individual tones of the chord to one wave - man perceive tones separately.
Only difference of the chord from a summary of single tones are bindings, ie. relations of bands belonging to tones.
|
1.The resounding of bands whose frequencies are
in ratios of small integers (approximately).
One band gains part of the potential energy from the other band; the measure of the transferred potential energy is called continuity of binding. |
2.The reactivity among the adjacent bands.
Energy of bands is consumed by power
that has a maximum at some small distance of two bands
(reminds Newton and Coulomb force).
The potential energy of the zones changes into the binding (kinetic) energy; the measure of change is called impulse of binding. |
During interaction of bands bindings arise and absorbs some of the energy bands. Let e.g. harmonic binding r12 between bands p1 and p2 mediates such interaction. It requires energy Ev for its existence, and the energy can be taken from nowhere else than from the bands p1 a p2. Potential energy of bands Ep gradually changes in the binding (kinetic) energy Ev.
Energy consumption in relation depends on the type of bond especially on the size of the musical interval. We assume that two basic processes exist. According to them, there are two types of interactions.
Conservation of energy
Consider two bands with initial energy E1=E2=E(0). Let c(s) is continuity of binding and i(s) impulse of binding, for formal interval s.
Binding of continuity transmits energy, thus energy is conserved:
Joule James Prescott| Joule James Prescott [džúl], 1818-1889, English physicist, one of the discoverers of the law of conservation of energy. |
E1 = E(1–c) E2 = E(1+c)
E1 + E2 = 2E
Binding of impulse energy consumes - energy decreases:
E1 = E(1–i/2) E2 = E(1+i/2)
E1 + E2 = 2E – i
(K.Asherov)
Impulse
Kinetic energy that is consumed by interactions of (close) band is called impulse of binding.
The largest impulse values are associated with the smallest intervals.
Direction of the impulse does not depend on the orientation of the binding;
value of the impulse is always positive.
The principle of impulse was introduced to musical practice long
before the principle of continuity.
But in music theory remained almost unnoticed.
In the 20 th century music theorists have pointed its existence
in several independent studies:
L.Janáček by connection of reconciliation
A.Schőnberg by economy of musical motion
K.Janeček in theory of imaginary tones.
K.Risinger by 2.principle of functional relations.
The impulse is a source of musical movement and the main factor acting on our feelings;
it adds color and density to chords and changes them to chaotic and dissonant.
Impulse ensures economy of movement of voices in the polyphony.
Impulse is the result of the energy interaction of bands; it is the energy consumed in bindings.
Continuity
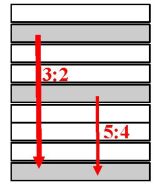
Binding has some continuity if its corresponding bands resonate. The greatest continuity in the formal system exists in case of ratios 3: 2, 5: 4 or some ratios derived from them (3: 4.5: 8) . Continuity will be denoted with the letter c.
The idea of continuity is not new.
Ancient Chinese theory says that each tone gives rise to a different tone - pure fifth.
J.P.Rameau considered the fifth as interval given by nature,
while upper fifths tone (g) returns to its source (c) at the end of the song.
According to his theory of fundamental bass - chords in fifths distances
creates meaningful harmonic sequences.
Continuity can also be found in considerations of other theorists:
in connection of exchange L.Janáček
in L.Bardos' principle of aliquote serie
in K.Risinger's 1.principle of functional relations
Rameau Jean Philippe| Rameau Jean Philippe [ramo], 1683-1764, French composer and music theorist considered as founder of classical harmony. He explains harmonic phenomena (thirds construction, authentic conclusion ...) through a series of overtones and resonance. The music is based on an approximation. The basis of the lowest common chord tone and relationshipsof chords are determined by the ratio of their fundamental tones. He laid the foundation stones of the theory of diatonic tonality and modulation. The melody must correspond with the harmony. |
Harmony with ties of continuity is quiet and consonant.
Music stream flows continuously without breaks.
A positive continuity highlights new content.
Direction of continuity
Continuity depends on the direction of action. According to the direction of links we distinguish direction of continuity. Continuity is positive or negative. Accordingly the direction of contninuity is direct or countercurrent. Continuity c has direction s = sign (c).
Continuity from frequency f1 to f2 is positive, if corresponding ratio f1/f2 has greater of prime characteristics in the numerator than denominator. E.g. 3/2 (or 3/4) as well as 5/4 (or 5/8) have positive continuity.
Illustration of characteristics
Coordinate system - continuity on the horizontal axis, impulse on vertical axis.
impulse (+)
c#
d
d#
e
f#
continuity(–) g e ß c à g# f continuity(+)
g#
a
b
h
identity
|prime (unison)
|
|halftone
|
|
|whole tone
|
impulse
|
| ..
|
| ..
| ... major third - quint - octave
|tritone
+---------- continuity ------------------ identity
Maximum impulse as well as maximum continuity tend to (octave) identity (ie. to prime or octave).
Cause of interactions
Energy bands
Due to inertia may basial membrane keep energy for a certain time.
Just as we have visual residuals from a longer observation of colored objects, we also can have residual hearing after listening to audio frequencies.
Continuity
Transfer of energy from one body to another is observed physically in phenomenon called resonance, in the study of forced oscillations. Body with certain operating frequency is vibrated, if a different body with close frequency is able to transmit energy. Such a phenomenon also occurs e.g. in decomposition of composite audio to harmonics using resonators.
The mechanism of energy transfer does not need to be linked to the sharing of energy of overtones. Interactions arising at basal membrane may internally absorb or release energy and create some energy relations (continuity).
When the membrane vibrates by effect of tone A and next tone B rises, is it possible that the tone B helps the membrane to vibrate(?), or conversely that the membrane helps vibrate to this tone?
Impulse
Coherence of the basal membrane may cause the inability to accept two slightly different waves. There is a limit - the minimum required difference, that implies relationships observed in the behavior of nearby tones (impulse).
characteristics of intervals
Boltzmann Ludwig Eduard| Boltzmann Ludwig Eduard [bolcman], 1844-1906, Austrian physicist, founder of the kinetic theory of gases and statistical physics, co-discoverer of black body radiation. |
Estimation of the values of characteristics
The masses and velocities of individual molecules of air as the whole, which fills a certain volume, manifest themselves as pressure and temperature. Similarly, it with the characteristics of harmonic relationships. The sum of effects of single bindings gives the resulting effect. Pressure and air temperature can be easily measured, but to assess the continuity of the harmonic current is difficult. For the continuity we must be derived from partial values continuity of individual bonds. The total value of the continuity must be derived from partial values continuity of individual bindings.
Many values in physics derives by similar manner (eg. we can only count, not directly measure the force acting between the sun and some of the planets ...)
|
Interval |
–5 |
–4 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Continuity |
–c1 |
+c2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
–c2 |
+c1 |
0 |
|
Impulz |
+i5 |
+i4 |
+i3 |
+i2 |
+i1 |
0 |
+i1 |
+i2 |
+i3 |
+i4 |
+i5 |
0 |
In the following paragraphs we will discuss the possibilities of determination partial characteristics..
We evaluate bindings corresponding to intervals of the 12-tone system by characteristics of continuity and impulse. Based on the derived values we try to generalize characteristics for all formal systems.
But it is not possible to deduce accurate values without knowledge of the nature of interactions between the bands. We know no method how to physically measure basic characteristics (continuity, impulse) or derived characteristics (entropy, ..). The only source are known root, [9], and various consonance amounts, [6], [9] of selected chords. According to them we will estimate certain values. On these then we will later demonstrate the nature of the proposed relationships.
Impulse
Estimation of values of impulse
Impulse I between two zones is a function of the energy E1, E2 and formal interval s. Tones are like bodies with gravitational or electro-magnetic fields:
I = f(E1,E2,s) = E1∙E2/g(s)
Interaction of bands is strong, if s is small.
In the simplest case, when E1 = E2 = 1, impulse depends only on
the formal size of the interval s: I = f(s).
The action of the impulse does not depend on the direction of linkage, the impulse is always positive.
We suppose the biggest impulse I at the intervals of semitone i1, whole tone i2 and minor third i3. Impulses of the next intervals i4, i5 seem to be negligible. At a distance of median of the system (μ = k div 2) is impulse supposed to be zero.
|
Interval |
–5 |
–4 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Impulz |
i5 |
i4 |
i3 |
i2 |
i1 |
0 |
i1 |
i2 |
i3 |
i4 |
i5 |
0 |
Distribution of energy
Consider two tones A, B with frequencies fA and fB, whose distance in octaves is x (K.Asherov). Suppose, force F(x) = –1/x² arises between A and B, which prevents their concurrent sounding. By integration F(x)dx we get energy E(x) = E0 + 1/x. If x=1/2, tak E = E0 – 2 = 0 a E(x) = 1/x – 2. For distance in halftones s is x = s/12 and E(s) = 12/s – 2. Energy of halftone E(1) = 12/1 – 2 = 10 and impulse is proportional to the energy i(s) ~ E(s), so for quadratic force distribution is:
i(s) = i(1)/E(1)∙(12/s –2)
where E(1)=10.
We can do this even for cubic or other hypothetical distribution. For cubic distribution of attraction is:
i(s) = i(1)/E(1)∙(288/s² –8)
where E(1)=280.
Impulse below the threshold of semitoneIf the impulse is inversely proportional to the distance x [octaves], i.e. i(x)~1/x, then for x >> 1 is i = 0. Somewhere around the border of semitone is impulse at maximum. But for x = 0 it appears to be again i = 0, i.e impulse of unison is zero. Impulse must accordingly growth to the maximum in the interval of a semitone 0-1.
Introduce exponential function i(s) = p∙sn/eqs e.g. for n=2. From derivation we find the maximum and then we can choose such constants p, q, to get extreme there where it should be.
Such function is for example:
i(s) = p∙(s²/e²s)
where p=88.7.
Values of impulse
s 1/s 1/s2 s2/e2s -------------------------- 1/2 26.40 49.03 8.15 1 12.00 12.00 12.00 2 4.80 2.74 6.50 3 2.40 1.03 1.98 4 1.20 0.43 0.48 5 0.48 0.15 0.10 6 0.00 0.00 0.02
Let's define value of impulse of semitone, e.g. i(1) = 12 and calculate the resulting values. We consider the function:
i(s) = 12/10 ∙(12/s –2)
i(s) = 12/280 ∙(288/s² –8)
i(s) = 88.7 ∙(s²/e²s)
Lost of energyBindins of tones that do not resonate have no reason to give energy. They could therefore e.g only balance energy of tones. But it seems that they rather drain energy from tones. We will try to find arguments for this assertion. Consider, every sound we can hear must have its own source of energy. When we are listening to two separate tones in a consonant interval or in such a distance that they do not interfere, we hear just these tones. But when we play halftone, we hear these tones, and something extra (disonance ...). What is it? (beats, noise, ..?) This effect must cost some energy (e.g. new tones that arise doe to beats must have its energy), and this energy must come from an energy source. Bute the only source of energy are the played tones.
Imaginary tones
Let us now proceed in Janeček theory of imaginary tones. When real tone G stops to sound, it is changing to an imaginary tone. This imaginary tone (G) can be canceled by: 1/ tone F# or G# or 2/ tone F.
Sometimes (according to K.Janeček) it may be canceled also by: 3/ tone A, but only in case, when the following conditions are satisfied:
- imaginary tone is not emphasized
- tone A is longer or more significant
- tone G is not preceded by tone F or F#
Assuming that impulse consumes energy of bindings, points 1-3 are understandable. To explain the difference between the tone G and A, we need extra help from Micka's preference for bass tones (in chapter Musical energy).
Critical anti-disturbing tone proves that impulse of semitone is greater than impulse of whole tone.
Dependence of impulse on height of tonesDoes impulse depend on the frequency? The human ear does not distinguish semitones in lower octaves the same way as in higher octaves. Beat frequency between f1 = 220 Hz and f2 = 224 Hz is f = f2 – f1 = 4 Hz. But two octaves above between f1 = 880 HZ and f2 = 896 Hz is 16 Hz. Smaller altitude shifts are more audible in the higher registers.
To each individual harmonic bindings of formal systems is assigned a value of the impulse. A summary of all values creates the matrix of impulse.
c c# d d# e f f# g g# a a# h
c 0 i1 i2 i3 0 0 0 0 0 i3 i2 i1
c# i1 0 i1 i2 i3 0 0 0 0 0 i3 i2
d i2 i1 0 i1 i2 1 0 0 0 0 0 i3
d# i3 i2 i1 0 i1 i2 i3 0 0 0 0 0
e 0 i3 i2 i1 0 i1 i2 i3 0 0 0 0
f 0 0 i3 i2 i1 0 i1 i2 i3 0 0 0
f# 0 0 0 i3 i2 i1 0 i1 i2 i3 0 0
g 0 0 0 0 i3 i2 i1 0 i1 i2 i3 0
g# 0 0 0 0 0 i3 i2 i1 0 i1 i2 i3
a i3 0 0 0 0 0 i3 i2 i1 0 i1 i2
a# i2 i3 0 0 0 0 0 i3 i2 i1 0 i1
h i1 i2 i3 0 0 0 0 0 i3 i2 i1 0
Continuity
Estimation of the values of continuity
Continuity c indicates the amount of energy flowing in the binding.
It is function of energy of bands E1,E2 and the formal interval s.
In the simplest case E1=E2=1 continuity depends
only on the formal interval s: c = C(s).
The highest continuity C is considered at interval of perfect fifth (resonance 3:2) and interval of major third (5:4).
Intervals of pure quart (4:3) and small sexta (8:5) are formally indistinguishable from intervals above.
Continuity depends on the direction of action.
The descending fifth C(–7)= C(+5)=+c1 has positive continuity.
Likewise the descending major third C(–4)=C(+8)=+c2.
Continuity of the other intervals is neglected.
|
Interval |
–5 |
–4 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Continuity |
-c1 |
+c2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-c2 |
+c1 |
0 |
Va = c(e->a) + c(c->a) - (i(e↔a)+i(c↔a))/2 Vc = c(e->c) + c(a->c) - (i(e↔c)+i(a↔c))/2 Ve = c(a->e) + c(c->e) - (i(a↔e)+i(c↔e))/2
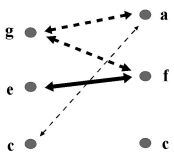
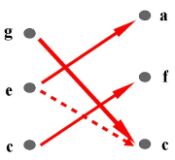
Approximate values of characteristics can be obtained even without measuring instruments. Let as play the A minor triad (a, c, e) and suppose most listeners will label tone a as root (regardless of octave position). From here we can conclude that there is a transfer of energy to the tone a. Using the energy values Va, Vc, Ve we write the condition for the transfer of energy to the tone a by two inequalities: Va >Vc, Va>Ve, i.e. Va =max(Va,Vc,Ve).
K. Risinger' gives conditions for determining roots of chords []. The following chords have the root C regardless of rollover (regrouping of tones), with condition, that tones are closest to each other (i.e. they are not affected by the octave positions) :
Triads: C-D-Eb, C-D-E, C-Es-G, C-E-G, C-F#-G, C-E-B, C-G-B,C-G-H
Tetrads: C-D-Eb-E, C-Eb-E-G, C-E-F#-G, C-Eb-G-H, C-E-G-B,C-G-B-H,C-D-E-G.
Pentads: C-D-Eb-E-G, C-Eb-E-F#-G, C-E-F#-G-B
Some of the chords do not say too much. But others are interesting. Let us notice two of them: C-Eb-G-H a C-G-B-H. Denote the values of the impulse
Value of continuity c1. - From bindings in chord C-Eb-G-H:
V(C) = c1–(i1+i3+i5)/2
V(Eb) = c2–c2–(i3+i4+i4)/2
where V(C)>V(Eb), i.e. c1>(i1+i5)/2–i4.
Value of continuity c2. From bindings in chord C-G-B-H:
V(C) = c1–(i1+i2+i5)/2
V(G) = c2–c1–(i3+i4+i5)/2
where V(C)>V(G) i.e. 2c1–c2>(i1+i2–i3–i4)/2
For exponencial distribution (see above paragraph Values of impulse) with approximate values i1=12, i2=6.5, i3=2, i4=0.5, i5=i6=0 vychází c1>12/2-0.5 i.e. c1> 5.5.
For c1= 6: 12–c2>(i1+i2–i3–i4)/2, and so c2 <12-(12+6.5-2-0.5)/2 i.e. c2 < 4.
We have derived unknown values of continuity from the values of impulse and observed roots of selected chords. In doing so, it confirms the basic assumption that the link (descending) major third (c2) is smaller than (descending) perfect fifth (c1).
|
i1 |
i2 |
i3 |
i4 |
c1 |
c2 |
ostatní |
|
12 |
6.5 |
2 |
0.5 |
6 |
3 |
0 |
To simplify further calculations we use the approximate values.
Sharing of bands
When mixing, timbre can - unlike the light - preserve to a certain extent an individual character.
Suppose a uniform distribution of intensities of tones and overtones and assign the same aliquot tones (of different chord tones) to the same bands. E.g. An aliquot e of both tones a and c (in chord f, a, c) is in the same band.
When all aliquot tones are only in bands, information, which tone has aliquots (and with what intensity) is lost. (We hear only the timbre of tones). Some tones help the other tones to sound. In our example tone c may use part of the total energy of tone a (with respect to band e).
Dependence of continuity on the pitch
Formal system does not distinguish octaves of tones and therefore continuity from c2 ke g2 (7 halftones) is the same as from c2 ke g1 (–5 halftones). And also the impulse between c1 and c#1 (1 semitone) is the same as between c1 and c# 2 (13 semitones). The octave is treated as unison.
This leads to a certain distortion, the characteristics also depends on octave position - the formal values therefore should be corrected.
A value of continuity is assigned to each individual harmonic bindings of formal system. A summary of all values creates the matrix of continuity.
c c# d d# e f f# g g# a a# h
c 0 0 0 0 -c2 +c1 0 -c1 +c2 0 0 0
c# 0 0 0 0 0 -c2 +c1 0 -c1 +c2 0 0
d 0 0 0 0 0 0 -c2 +c1 0 -c1 +c2 0
d# 0 0 0 0 0 0 0 -c2 +c1 0 -c1 +c2
e +c2 0 0 0 0 0 0 0 -c2 +c1 0 -c1
f -c1 +c2 0 0 0 0 0 0 0 -c2 +c1 0
f# 0 -c1 +c2 0 0 0 0 0 0 0 -c2 +c1
g +c1 0 -c1 +c2 0 0 0 0 0 0 0 -c2
g# -c2 +c1 0 -c1 +c2 0 0 0 0 0 0 0
a 0 -c2 +c1 0 -c1 +c2 0 0 0 0 0 0
a# 0 0 -c2 +c1 0 -c1 +c2 0 0 0 0 0
h 0 0 0 -c2 +c1 0 -c1+c2 0 0 0 0
Characteristics of modalities
|
- |
c |
d |
e |
f |
g |
a |
h |
|
c |
0 |
+2 |
+4 |
+5 |
–5 |
–3 |
–1 |
|
d |
–2 |
0 |
+2 |
+3 |
+5 |
–5 |
–3 |
|
e |
–4 |
–2 |
0 |
+1 |
+3 |
+5 |
–5 |
|
f |
–5 |
–3 |
–1 |
0 |
+2 |
+4 |
+6 |
|
g |
+5 |
–5 |
–3 |
–2 |
0 |
+2 |
+4 |
|
a |
+3 |
+5 |
–5 |
–4 |
–2 |
0 |
+2 |
|
h |
+1 |
+3 |
+5 |
+6 |
–4 |
–2 |
0 |
Continuity of modality
We show calculation of continuity of modality on the example of natural modality [c,d,e,f,g,a,h]. In the table of intervals is number 5 (+5 or –5) on each row. Each tone of the natural modality has fifths ratio to at least one other tone.
|
c |
d |
e |
f |
g |
a |
h |
|
|
K |
2 |
2 |
2 |
1 |
2 |
2 |
1 |
|
T |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
The value of continuity is a function of fifth intervals and interval of major third.
In total there are N=7²=49 intervals in the natural modality, of which is 12 fifths (K) with continuity c1 and 6 major thirds (T) with continuity c2.
To quantify specific examples we will use values c1=2,c2=1. The total (absolute) mean continuity of natural modality is ∑s=12*c1+6*c2=30.
For comparison - continuity of Gypsy modality is 8*c1+10*c2=26, continuity of harmonic minor as well as podhalské-folk makes (8*c1+8*c2)=24.
Relative continuity with respect to all bindings makes in natural heptatonic s=∑s/N= 30/49=0.61. Relative continuity serves to compare modalities with different numbers of tones.
E.g. natural pentatonic 2322(3) has total continuity 8*c1+2*c2=18 and relative continuity s=∑s/N= 18/25=0.72. Natural pentatonic thus has relatively higher continuity than natural heptatonic.
Continuity related to tones
|
K |
T |
Continuity |
Continuity of tone |
|
|
c |
2 |
1 |
2c1+c2 |
5/30=16.67% |
|
d |
2 |
0 |
2c1 |
4/30=13.33% |
|
e |
2 |
1 |
2c1+c2 |
5/30=16.67% |
|
f |
1 |
1 |
c1+c2 |
3/30=10% |
|
g |
2 |
1 |
2c1+c2 |
5/30=16.67% |
|
a |
2 |
1 |
2c1+c2 |
5/30=16.67% |
|
h |
1 |
1 |
c1+c2 |
3/30=10% |
By continuity relative to the tone we mean the value (in percentage) how much the given tone contributes to the overall continuity of modality.
In the natural modality - tones c,e,g,a contributes mostly to continuity (are linked with the other two fifths and one major third one) - they cover the 2/3 of the total continuity.
Two successive tonalities stabilized gradually in the natural modality - major and Aeolian minor.
Tonic (see Harmonic functions) of the major C key is chord [c,e,g], tonic of minor key chord [a,c,e]. Also whole tetrad [c,e,g,a] appears as tonic in the newer music.
Comparison with the distribution of continuity in other modalities:
|
Natural |
Podhalská |
Harm. minor |
Gypsy |
|
|
Schéma |
221222(1) |
221212(2) |
212213(1) |
213113(1) |
|
Modalita |
cdefgah |
cdefgg#a# |
ahcdefg# |
ahcd#efg# |
|
∑ |
5 4 5 3 5 5 3 |
6 3 2 4 4 2 3 |
5 2 4 2 6 3 2 |
3 3 4 3 6 3 4 |
|
Maxima |
c,e,g,a |
c,f,g |
a,c,e |
c,e,g# |
We have stated Gypsy modality in the form in which it is closest to the harmonic minor. High continuity of tone e appears to indicate that this shape may not be essential.
They are usually given two shapes: gypsy major 131213(1) a gypsy minor 213113(1). As basic shape is considered Indian bhairava 131213(1) (according to that teaches all the other transpositions). In succession efg#ahcd# has the start tone e the highest continuity.
Distortion of tone by impulse
Let us now consider further that continuity relative to the individual tones
is canceled by impulse bindings.
Therefore, we define the binding influence of the tone by relatíon:
b = f( |c|, i)
where b is binding influence, |c| absolute value of continuity, i impulse and f is some function.
(Matrix of influences is a functions of matrices of continuity and impulse B = g(C,I)).
Consider for example the following values of binding influences:
|
Interval |
–5 |
–4 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Binding influence |
+4 |
+2 |
–1 |
–1 |
–2 |
0 |
–2 |
–1 |
–1 |
+2 |
+4 |
0 |
|
- |
c |
d |
e |
f |
g |
a |
h |
∑ |
|
c |
0 |
–1 |
+2 |
+4 |
+4 |
–1 |
–2 |
+6 |
|
d |
–1 |
0 |
–1 |
–1 |
+4 |
+4 |
–1 |
+4 |
|
e |
+2 |
–1 |
0 |
–2 |
–1 |
+4 |
+4 |
+6 |
|
f |
+4 |
–1 |
–2 |
0 |
–1 |
+2 |
–2 |
0 |
|
g |
+4 |
–1 |
–1 |
–1 |
0 |
–1 |
+2 |
+7 |
|
a |
–1 |
+4 |
+4 |
+2 |
–1 |
0 |
–1 |
+7 |
|
h |
–2 |
–1 |
+4 |
–2 |
+2 |
–1 |
0 |
0 |
Potential of the band
Sum of the effects b of individual bindings to the given tone (the energy band) is called a potential of tone in modality (formal potential, F-potential).
U(i) = ∑b(hi,j)
where h is formal interval and i,j ε (0,k–1), j!=i. Potential depend on the direction of continuity. F-potential is sum (see the last column) of B-influences (in rows):
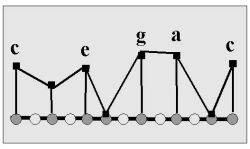Potentials of bands of natural modality:
U(g) = U(a) = 7.0 U(c) = U(e) = 6.0 U(d) = 4.0 U(f) = U(h) = 0.0
We see essentially the same results we have derived above: tones {c, e, g, a} have the greatest F-potential.
Effect of orderliness of harmonyIn the interaction of more than two bands we expect - besides partial effects - also effect of the overall entropy of the chord. Better organized grouping of tones (consonance) loses less energy.
Let m be the binary vector of modality and U matrix of potentials. Vector represents F-potentials of modality tones: u = m∙U.
Potential
We enumerate formal potentials of individual bands according to the binding influences
(total formal potential in the last column is the sum of the partial B-influences in the row).
Tones
- fixed ( c,e ) => tonic
- sensitive ( f,h )
- bound ef, hc (like Earth-Moon pair)
- free ( g,d,a) tones
Tones - quiet ( for melodic endings ) vs. restless ( mostly h , d ),
Tones - fixed vs. sensitive vs. free (according to potentials...)
Primary bands
From the k bands of the formal system we select such a p bands.
that have their energy directly from the tones (primary, P-bands).
Other, minor bands (secondary, S-band) obtain their energy through bindings.
Linkages between bands PP, PS SS (SP) have different meanings,
the most important for us are bindings PP.
If given musical phrases keeps a certain modality then some bands remain
for all the time without energy intake,
but - due to the redistribution of energy - not empty.
Assuming that the energy input into the P-zones is balanced,
we can infer some characteristics just from the modality structure.
If we consider also interaction of secondary bands (bindings PS), we obtain these values: g,a: 7; c,e:6; d:4; f,h:0; f#,a#:–2; g#, d#, c#:–4. Selected chords of natural modality have the following formal potentials: P( C) = P(Ami) = 6.33; P( Emi) = P( F) = 4.33; P( Dmi) = P(G) = 3.67; P( Hmi5–) = 1.33. Values are determined to one tone, eg. for C: P(C)=(c, e, g) = [P(c)+ P(e)+ P(g)]/3 = (6+6+7)/3 = 6.33. Among the so-called tonal skeletons P.Panoff mentioned these structures: 2212(5), ie.[c,d,e,f,g] and 2122(5), ie.[c,c#,d#,f,a#], both with the root c. The tone c has really a high potential in the first of the structures (tones make series c, g, d, f, e according to their potentials). But in the second structure tone f acquires domination (according to our definition of potential) (tones make series f,a#, d#,c,c#).
Until now, we considered only the primary bands, ie the bands corresponding to the tones of modality. The following table calculates also potentials of secondary bands.
modality: 1 0 1 0 1 1 0 1 0 1 0 1 | formal
tones: c c# d d# e f f# g g# a a# h | potential
-----------------------------------------------------
c 0 –1 +2 +4 +4 –1 –2 | +6 c
c# –2 –2 –1 +2 –2 +2 –1 | –4 c#
d –1 0 –1 –1 +4 +4 –1 | +4 d
d# –1 –2 –2 –1 +2 –2 +2 | –4 d#
e +2 –1 0 –2 –1 +4 +4 | +6 e
f +4 –1 –2 0 –1 +2 –2 | 0 f
f# –2 +2 –1 –2 –2 –1 +4 | –2 f#
g +4 +4 –1 –1 0 –1 +2 | +7 g
g# +2 –2 +2 –1 –2 –2 –1 | –4 g#
a –1 +4 +4 +2 –1 0 –1 | +7 a
a# –1 +2 –2 +4 –1 –2 –2 | –2 a#
h –2 –1 +4 –2 +2 –1 0 | 0 h
Potentials of all bands of the natural modality:
U(g) = U(a) = 7.0, U(c) = U(e) = 6.0, U(d) = 4.0,
U(f) = U(h) = 0.0, U(f#)= U(a#)=–2.0, U(c#)= U(d#)=U(g#)=–4.0
Object in context
Progression of objects
Let us have a progression of objects A,B,C..., having certain natural properties (states) defined with help of vectors a,b,c,...Objects are adaptable. Under influence of his predecessor the object X change its state to x'. In our example it comes on a,b',c',....
If the object has plenty of time, it converges back to its natural state. E.g. a,b',c' -> c.
We assume, 2 processes exist:
Influences of objects: c'= c * T(b,c), where T is transformation matrix. Convergence of object: c = c' * Ni, where N is convergence matrix and i number of steps. (After time interval dt we always multiply vector c'(i) again by matrix N.) The aim is to find for each object x such convergence matrix, thatlim(x'*Ni)=x, for a finite integer n, i->n.
Characteristic equation
If object accomplish its natural state, than convergence does not change it:
N * c = 1 * c.
This equation is a special case of characteristic equation:
N*c = b *c, where c is characteristic vector
and b characteristic number (b=1).
Musical stream
Let us apply the mentioned draft to musical stream.
Every chord has elementary characteristics (potentials of tones, continuity, impulse, ...),
and in consequence also certain real characteristics (sonance, genus, ...).
In context all this characteristics change.
E.g. chord G by himself sounds unlike the chord G in sequence F-F#-G.
We acquire the perception of pure G only after certain time of convergence.