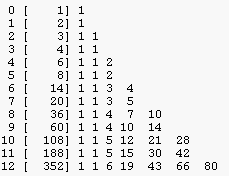Schematic algebra - G-Systems

G-Systems - An algebraic theory of musical structures
Combinatorics of necklaces...
AbstractAn algebraic theory of chord structures is being presented in this paper. Every tone grouping is depicted as an instance of the so-called G-system. The aim is to provide a simple algorithm for a generation of musical structures. It should be useful for programmers of computer music as well as for those interested in musical analysis. The theory of G-systems gives some known mathematical results in a simple and clearly organized way. Therefore it might be inspiring for mathematicians studying methods of enumeration, theory of groups, algebraic solutions of combinatorial problems and other areas (Fermat's theorems, Gauss' theory of equation classes, Polya's enumeration, Sylowov's groups,..).
1.G-system and its instances
The area we are studying here is in the combinatorial theory known as Combinatorics of necklaces.
1.1 Elementary definitions
Let us think about arranging n elements into k cells. Let A be a set with n members (elements) and the set E(A) = {0, 1, .., n-1} the base of A. Let B be a set with k members (cells) and ξ relation from E(B) to E(A).
ξ
(cells) E(B) ------------- E(A) (elements)
Let numbers E(B) be positions of numbers (digits) from E(A).
Written in n-number system we obtain nk possible numbers. Let the
set of all these numbers be marked M()= M(n,k). Members of this set
are so called instances.
E.g. the sets A={p, q}, B={x, y, z} have E(A)={0, 1}, E(B)={0, 1,
2} as their bases. The system M(2,3) has 23=8 instances {000,
001,.., 111}.
Let us call the set M()=M(n,k) (with relation ξ) system of degree n
and order k. If ξ is equivalence relation one can distinguish some
instance classes. The classes are the result of decay M()/ξ. Each
class has its representative number. Number of transpositions means
the number of members in a class.
In case of 12-tone tempered musical system we have n=2, k=12. E.g.
let A={exist, non-exist} and B={c, c#, d, d#, e, f, f#, g, g#, a,
a#, h} . The bases E(A)={0, 1}, E(B)={0, 1, .., 11} and the ξ
relation forms the system M(2,12). The instance 001001001001
represents tone groupings [c, d#, f#, a] and has two transpositions
010010010010, i.e. [c#, e, g, a#] and 100100100100 i.e. [d, f, g#,
h]. The diminished seventh chord is a class of M(2,12) with 3
transpositions.
1.2 G-relation
Let relation G, defined as follows, be called G-relation.
u(i,j) = nj * g(i) ( mod(r-1))
Number r is (in this article) always assumed to be equal to the total number of instances, i.e. r = nk. Number g(i) is representative number, u(i,j) are instance numbers.
Systems with the G-relation we name G-systems, G()=G(n,k). Every G(n,k) has m(n,k) classes marked g(i), i=1..m.
1.3 Instance numbers
Let us write an outline of all instances ordered by classes. The outline of G(n,k) has k columns (k is the maximum transposition count). The 16 instances of G(2,4) make 6 classes.
Instances of G(2,4)
| 1 |
0 0 0000 0
0 0
|
| 2 |
0 0 0 1 1 0 0 0 0001 0010 0100 1000 1 2 4 8
0 1 0 0 0 0 1 0
|
| 3 |
0 1 1 1 1 0 0 0 0011 0110 1100 1001 3 6 12 9
0 1 0 0 1 0 1 1
|
| 4 |
1 0 0 1 0101 1010 5 10
0 1 1 0
|
| 5 |
1 1 1 1 1 0 0 1 0111 1110 1101 1011 7 14 13 11
0 1 1 0 1 1 1 1
|
| 6 |
1 1 1111 15
1 1
|
1.4 Generation of instance numbers
The algorithm is similar to the Eratosthenes' sieve for separating primes from natural numbers. In our case we separate numbers of classes representatives from all instance numbers. Instance transpositions are analogies of prime multiples in Eratosthenes' sieve.
empty set M
↓
+--+- for g=0 to (nk-1-1) -- write the last class
| | | g=nk-1
| ↑ is class g in M ?
| | |
| +- YES-----+
| |NO
| |
| write g to M
| ↓
| instance u <- g
| |
|+---> while not u in M ----+
|| | |
|| write u to M |
|| | |
|| instance transposition |
|| u <- n * u |
|+------<-----+ |
+-------------<-------------+
Examples of the output:
G(n,1)
G(2,1) G(3,1) G(4,1)
0 0 0
1 1 1
2 2
3
G(2,2) G(3,2) G(4,2)
0 0 0 6 9
1 2 1 3 1 4 7 13
3 2 6 2 8 10
4 3 12 11 14
5 7 5 15
8
G(2,3) G(3,3) G(4,3)
0 0 0 21
1 2 4 1 3 9 1 4 16 22 25 37
3 6 5 2 6 18 2 8 32 23 29 53
7 4 12 10 3 12 48 26 41 38
5 15 19 5 20 17 27 45 54
7 21 11 6 24 33 30 57 39
8 24 20 7 28 49 31 61 55
13 9 36 18 42
14 16 22 10 40 34 43 46 58
17 25 23 11 44 50 47 62 59
26 13 52 19 63
14 56 35
15 60 51
1.5 Divisibility in G(n,k)
Instance number u(i,j) is prime relative to r -1 = nk -1 only if
corresponding class number g(i) is prime relative to r -1. The
number of all instances that are primes relative to r -1 is φ(r),
where φ is the Euler function. If g(i) is prime relative to r -1,
then its class must be the self class (not nested) and such class
has k instances.
Therefore: φ(nk -1)= 0 (mod k)
In G(2,4) only these instances are prime numbers relative to 24
-1=15: (1, 2, 4, 8) and (7, 14, 13, 11). And φ(24 -1) = φ(15) = 8;
8 = 0 (mod 4).
2.Enumeration of classes
One of the first solutions to the problem we are studying was published by Gauss in his algebraic theory of equation classes [Gauss,1959]. Polya presented a general combinatorial solution of counting structures. His theorem of enumeration [Preparata,1974] was designed for counting of classes with regard to arbitrary operations of symmetry. Musical chord structures have only one such operation - rotation. This fact allows us to apply a simple algorithm.
2.1 Nesting
For each d|k there exists a system G(n,d) nested to the G(n,k). The
nested class g' in G(n,k) is similar to its original class g from
G(n,d). Truly original classes are called self-classes. The
similarity to the original classes means the same number of
transpositions and similar instance structures. The system G(n,p),
p is prime, has just one nested system G(n,1). For g from G(n,d),
g' from G(n,k), d|k it holds: g' = c . g where c is nesting
quotient defined as follows:
c(d,k) = (nk-1) / (nd-1). For example, the system G(2,6) inherits
the nested systems G(2,1), G(2,2) a G(2,3);
G(2,1) is also nested into G(2,2) and G(2,3).
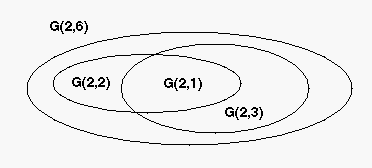
Other example: the system G(2,4) inherits the nested systems G(2,1) and G(2,2); see e.g. class g(2) = 1 in G(2,2) and its corresponding class g(4) = 5 in G(2,4) with nesting quotient c(2,4) = 5.
G(2,1): g(1)= u(0,1)= 0 g(2)= u(0,2)= 1
G(2,2): g(1)= u(0,1)= 0 g(2)= u(0,2)= 1 u(1,2)= 2 g(3)= u(0,3)= 3
G(2,4): g(1)= u(0,1)= 0 g(2)= u(0,2)= 1 u(1,2)= 2 u(2,2)= 4 u(3,2)= 8 g(3)= u(0,3)= 3 u(1,3)= 6 u(2,3)=12 u(3,3)= 9 g(4)= u(0,4)= 5 u(1,4)=10 g(5)= u(0,5)= 7 u(1,5)=14 u(2,5)=13 u(3,5)=11 g(6)= u(0,6)=15
G(2,1) - G(2,2): c(1,2) = (22 -1) / (21 -1) = 3 G(2,2) - G(2,4): c(2,4) = (24 -1) / (22 -1) = 5
2.2 Recurrent relations
Let v(n,k), w(n,k) and m(n,k) be the number of self, nested and all
classes in G(n,k). It is hold:
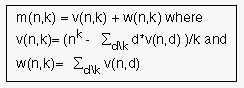
Specially for prime p is:

E.g. The system G(2,6) has 14 classes (9 self-classes + 5
nested-classes):
Counting of classes in G(2,6)
|
Self classes |
Nested classes |
|
v(2,1)=2/1=2 |
w(2,1) = 0 |
|
v(2,2)=(22-1v(2,1))/2= 1 |
w(2,2) = v(2,1) = 2 |
|
v(2,3)=(23-1v(2,1))/3= 2 |
w(2,3) = v(2,1) = 2 |
|
v(2,6)=(26-1v(2,1)-2*v(2,2)-3*v(2,3))/6 = 9 |
w(2,6) = v(2,1)+v(2,2)+v(2,3)= 5 |
Therefore m(2,6)= v(6) +w(6) = 9 +5 = 14 classes.
Gauss [CG1} has put the previous recurrent equations in an elegant, compact form: nk = ∑ d(d) i.e. in our terminology: nk = ∑{d|k} d*v(n,d).
2.3 Simplifying
Let us evaluate the totals of all classes m(n,k) for particular orders k as functions of n:
k=1: m(n,1)= 1/1 (n) + 0 = n k=2: m(n,2)= 1/2 (n2- n)+ n = 1/2 (n2+n) k=3: m(n,3)= 1/3 (n3-n)+ n = 1/3 (n3+ 2n) k=4: m(n,4)= 1/4 (n4-n2)+ 1/2 (n2+n) = 1/4 (n4+ n2+2n) k=5: m(n,5)= 1/5 (n5-n) + n = 1/5 (n5+ 4n) k=6: m(n,6)= 1/6 (n6-n3-n2+n)+1/6(2n3+3n2+n)= 1/6 (n6+n3+2n2+2n) k=7: m(n,7)= 1/7 (n7-n) + n = 1/7 (n7+ 6n) k=8: m(n,8)= 1/8 (n8-n4)+ 1/4(n4+n2+2n)=1/8(n8+n4+2n2+4n)
In case of rotational operations Polya's theory gives this result [Beckenbach,1964]:
m(n,k) = 1/k ∑{d|k} φ(d)* nk/d (including d=k),
where φ is the Euler function.
3.Compositions of G-systems
3.1 Segmentation
The nesting (shown in the previous paragraphs) is a matter of
G-systems with constant n.
Now we are going to study G-systems with constant k. These systems
also have something in common.
E.g. let us see the systems G(2,2) and G(3,2). The latter is only
an extension of the former.
G(3,2) as an extension of G(2,2)
G(2,2) = G(3,2)
0 0
1 2 1 3
3 4
6 2
7 5
8
|
Every G(n,k) has n classes nested from G(n,1). Let us assume, these
classes separate the G-system into segments. Let s (s<n )=""
such="" a="" representative="" of="" this="" segment="" s="" is=""
the="" number="">
g(s) = (n-s) * (nk-1) / (n-1).
If a segment exists in G(n,k) then a similar segment exists also in
G(n+1,k). This idea becomes clearer if we rewrite all the numbers u
with the numbers (nk-1)-u.
Segmentation of G(3,3)
u
0 segment 2
1 3 9
2 6 18
4 12 10
5 15 19
7 21 11
8 24 20
------------------
13 segment 1
14 16 22
17 25 23
------------------
26 segment 0
|
(nk-1)-u = 27-u
0 segment 0
------------------
9 1 3
12 10 4
13 segment 1
------------------
18 2 6
19 5 15
21 11 7
22 14 16
24 20 8
25 23 17
26 segment 2
|
3.2 Number systems
Let us write the numbers nk-1-u from the previous table as functions of n and take interest in quotients of the polynomials:
k=2 k=3
segment 0 segment 0
1 1
segment 1 segment 1
n 1 n2 1 n
n+1 n2+n n2+1 n +1
n2+n+1
k=2 k=3
segment 0 segment 0
0 0 0 0 0
segment 1 segment 1
1 0 0 1 1 0 0 0 0 1 0 1 0
1 1 1 1 0 1 0 1 0 1 1
1 1 1
Each G-system is a set of numbers from the n-th number system. The G-relation separates G(n,k) into n segments, where every segment s uses always just s symbols, s=0..n-1.
Compositions of G-systems
G(1,2) 00 00 00
----------------------------
10 01 10 01 10 01
G(2,2) 11 11 11
----------------------------
20 02 20 02 20 02
21 12 21 12 21 12
G(3,2) 22 22 22
----------------------------
30 03 30 03
31 13 31 13
32 23 32 23
G(4,2) 33 33
----------------------------
40 04
41 14
42 24
43 34
G(5,2) 44
----------------------------
|
G(1,3) 000 000 000
--------------------------------------------
100 001 010 100 001 010 100 001 010
110 101 011 110 101 011 110 101 011
G(2,3) 111 111 111
--------------------------------------------
200 002 020 200 002 020
201 012 120 201 012 120
210 102 021 210 102 021
211 112 121 211 112 121
220 202 022 220 202 022
221 212 122 221 212 122
G(3,3) 222 222
--------------------------------------------
300 003 030
301 013 031
302 023 032
310 103 130
311 113 131
312 123 132
320 203 230
321 213 231
322 223 232
330 303 330
331 313 331
332 323 332
G(4,3) 333
--------------------------------------------
|
The sum of polynomial quotients is the same for all instances of a given class (the instances of a class have the same level).
4.Binary G-systems
Binary system G(2,k) is a special case of G-system, n=2. It is suitable for classification of musical structures.
4.1 Distance schema
In a binary system (base E(A) ={0, 1}) it is easy to express
structure of instances.
Let level of class L be the number of digits "1" in an instance and
let interval be the distance between two digits "1". Distance
schema is the list of all neighboring intervals, last interval in
brackets, [Janecek,1959].
Distance schema of instances in G(2,4))
i g(i) Instance numbers (binary) Schema Level ------------------------------------------------------ 1 0 0000 (0) 0 2 1 0001 0010 0100 1000 (4) 1 3 3 0011 0110 1100 1001 1(3) 2 4 5 0101 1010 2(2) 2 5 7 0111 1110 1101 1011 1 1(2) 3 6 15 1111 1 1 1 (1) 4 |
4.2 Triangles
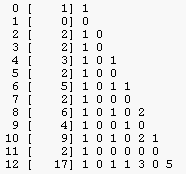
The last column in the previous table displays the level of the corresponding class i.e. level of instances of the class. Let us count how many instances and classes there are on each level.
Counting in G(2,4)
Level 0 1 2 3 4 ----------------------------------------- All instances 1 4 6 4 1 Nested instances 1 0 2 0 1 Self instances 0 4 4 4 0 ----------------------------------------- All classes 1 1 2 1 1 Nested classes 1 0 1 0 1 Self classes 0 1 1 1 0 |
The following diagrams display the same (structured into triangles)
for all G(2,k). The first column displays the order k of given
G-system, in the next columns are the counts for particular levels.
The last columns have the totals of instances or classes. The
triangles are symmetrical, we write only half of them.
E.g. in 12-tone music there are 220 triads in 19 classes. These 19
classes mean that 19 types of triads exist (minor, major,
augmented, diminished, ...). One class only (the augmented triad)
is nested. This class has 4 instances. Therefore there is 220-4=216
self-instances of triads and 216/12 = 19-1 = 18 self-classes of
triads.
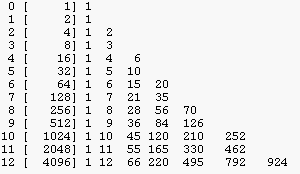
k (0)(1)(2)(3) (4) (5) (6) (7) (8) (9)(10)(11)(12) ---------------------------------------------------------------------- 12 1 12 66 220 495 792 924 792 495 220 66 12 1 all instances ---------------------------------------------------------------------- 1 1 1 2 0 2 0 3 0 3 3 0 nested instances 4 0 4 4 4 0 6 0 6 12 18 12 6 0 ---------------------------------------------------------------------- 12 0 12 60 216 480 792 900 792 480 216 60 12 0 self instances 12 0 1 5 18 40 66 75 66 40 18 5 1 0 self classes ---------------------------------------------------------------------- 1 1 1 2 0 1 0 3 0 1 1 0 nested classes 4 0 1 1 1 0 6 0 1 2 3 2 1 0 ---------------------------------------------------------------------- 12 1 1 6 19 43 66 80 66 43 19 6 1 1 all classes
Self-instance and self-classes triangle
|
|
|
Nested instance and nested classes triangle
|
|
|
All instance (Pascal triangle) and all classes triangle
|
|
|
The total number of nested instances as well as nested classes in a
system with prime k is equal to 2. Number of self-instances is
always the k-multiple of the number of self-classes.
more
Conclusion
In this paper we presented an insight into the problem of musical
structures. Our results were compared with similar results obtained
by Gauss and by Polya. The theory of G-systems also has some
connections to others mathematical areas.
E.g. a
restriction of
G-systems
(r<nk) leads to the theory of primitive roots;
the distribution of prime numbers
in particular classes might give some information
about primes;...
Particularly,
the
triangle of self-classes
might be interesting. Some theorems
about primes (Wilson theorems,...) are connected with its
structure. The triangle seems to be more general then Pascal
triangle - the latter can be obtained by an integration of members
from the former.
The theory of G-systems was presented at the poster session of the
Conference on Computational and Mathematical Methods in Music,
Vienna, December 1-4, 1999 (Diderot Forum on Mathematics and
Music). The text, which follows, covers and extends the one printed
in the conference proceedings.
At the beginning I called these systems by a term "Genetic
systems", because of certain analogy with inheritance (see Nesting
of G-systems). Later I have shortened the name to "G-systems". I
worked on this theory mostly in the years 1990-1992. In the
following years, 1993-1996, I looked for a similar theories in the
literature.
The enumeration of total number of G-system classes is the same as
the enumeration of total number of equation classes, which was
studied by Carl Fridrich Gauss nearly 200 years ago. So the letter
G in the name "G-system" would be connected with Gauss. He was
probably the first one who knew and described these mathematical
constructions.
Bibliography
Gauss,1959 Gauss Carl Fridrich: Trudy po teorii cisel (Ucenie o
vycetach II),p.782) (Works on Theory of Numbers; in Russian),
Moscow 1959.
Janecek,1959 Janeček Karel: Základy moderní harmonie (Fundamentals
of Modern Harmony; in Czech), Prague 1965.
Beckenbach,1964 Edwin F.Beckenbach, George Polya: Applied
Combinatorial Mathematics University of California, John Wiley and
Sons,Inc , New York, 1964.
Preparata,1974 Franco P.Preparata, Raymond T.Yeh Introduction of
Discrete Structures Addison-Wesley Publishing Company Inc., U.S.A.,
1974.