Music theory - Harmonic bindings

Romanian translation of this web page (supported by Web Geek Science)

Abstract

The paper submits a musically theoretical model of relations among the tones in the harmonic music stream.
Energy bands (zones) are associated with the tones of a regular musical system. The bands influence each another, the bindings exhausting energy from the bands.
Two basic interactions are assumed:

Reactivity: the energy discharges mostly by way of bindings; the measure of this energy is the so called impulse of binding (binding impulse).
Sharing of energy: one band gives the energy over to the other one; the quantity of the energy given over is the so called continuity of binding (binding continuity).

Some characteristics of chords are derived from the model (root, entropy, genus) as well as possible explanation of selected harmonic and melodic relations. The modality is defined and inferring of its harmonic functions is suggested.

The model is applied to the 12tone system. The octave identity is the basis of the so called formal system. In this system the perfect fifth has the maximum continuity. The semitone is the carrier of the maximum impulse. The major and minor triad serves for the explanation of the root, entropy and genus of the chord.
A few remarks concerning the harmony and melody analysis are also present. The progression continuity known from the baroque style is evaluated. Model is used for the generation of the harmonic music stream.
Model unifies the Janeček's theory of imaginary tones [Janeček,1965] with the two Risinger's principles of functional relations [Risinger,1969].
The contribution could be of interest for the theorists in musical and natural sciences - dealing with the formalization of musical structures, perception, theory of information coding and the like.

Content

1. Introduction
2. Model
3. Implementation
4. Application of the model
- 4.1 Musical style
- 4.2 Algorithmic composition
Conclusion
Bibliography

1. Introduction

Our work starts especially from the works of Czech and Slovak music theorists - namely from the theory of linking of chords by Leoš Janáček, [4], and the theory of harmonic functions by Otakar Šín, [10].

Some concepts we are using are taken from the physics. We do not mean, however, the described phenomena are of physical nature only. The reality is measurable: we express the relations observed in musical compositions numerically. We do not discuss the substance of the phenomena, though. The values of the parameters in our model, derived from the empirical materials, are fuzzy; but the question of a detailed mathematical model remains open.

We have concentrated our attention to harmony. The position of harmony is, in a sense, special. Harmony is the element of musical expression and at the same time it is something more general, that binds other elements, [12]. The analysis of harmony is usually more successful, [7], than e.g. the analysis of melody. The actions of harmony phenomena can be most easily determined in the tonal context, [3]. The tonality is always made of a certain modality, [13], - and modalities emerge within harmonic systems (musical systems). In western cultures the music composed in 12-tone system prevails, but there are cultural areas using other systems; theories not only confirm those systems, [8], but predict possible future ones as well. We have created a theory independent of musical system. Our model was designed for the systems dividing the octave interval in equal portions; the resulting model is simple and easily algorithmizable.

2. Model

2.1 Harmonic system

Harmonic system is a relation on a set of tones. If tones frequencies are ordered in the geometric progression, we speak about the regular harmonic system, [8].
more on musical systems

Interactions

Let the energy zone (energy band) be a carrier of the energy pertaining to the given frequency. The energy of each tone in the system does not vanish at the moment the tone stops to sound (we speak about psycho-acoustic phenomena, too). The cumulated energy remains in the zones until external forces exhaust them. We assume the following external forces:

Environment resistivity: it causes a gradual loss of energy in the zones.
Interactions among the zones: they redistribute and exhaust energy of zones.

The interaction depends especially on the size of the musical interval .
Let the harmonic binding be a carrier of the energy pertaining to the given musical interval.

We assume that two basic processes exist:

Continuity:

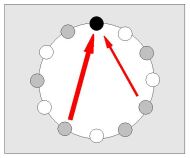
1.The resounding of zones whose frequencies are in ratios of small integers (approximately). One zone gains part of the potential energy from the other zone; the measure of the transferred potential energy is called continuity of binding .

Impulse:

2.The reactivity among the adjacent zones. The potential energy of the zones changes into the binding energy; the measure of change is called impulse of binding .

Formal system (F-system) is defined as a system in which the tones with the frequencies in the 2:1 ratio are considered to be equal (octave identity). Each tone of F-system stands for a class of equivalent tones of the regular system. Hence, the regular system breaks in the equivalence classes with a constant number, k, of portions. Let us call the number k the order of the system. Formal intervals (F-intervals) only, i.e. the intervals not exceeding the system order, make sense in the formal F-system.
more on music energy

2.2 Tonality

Tonality

Modality is a subset of F-system tones. It means that we select p primary zones (P-zones) which have their energy directly from the sounding tones. The other zones, secondary zones (S-zones), gain their energy through bindings only. If we assume that the energy input in the P-zones is balanced, we can derive some characteristics from the modality structure itself.
more on tonality

Formal potential (F-potential) of a zone is the sum of individual bindings influences (B-influences) going from other zones to the given zone.

Tonality is a modality with some restrictions on possible groupings. The set of all groupings in a tonality is the harmonic variety.

Every grouping has its specific properties depending on its position within the tonality. The F- potential of the grouping is a sum of the F-potentials of the zones taking part in it. We call tonicity of the grouping the F-potential reduced by the entropy of the sounding.

Harmonic functions

Harmonic functions are groupings from a harmonic variety with extreme properties. They are defined as follows:

Tonic (T) is the grouping with the maximum tonicity.
Dominant (D) is the grouping with the maximum positive continuity towards the tonic.
Subdominant (S) is the grouping with the maximum negative continuity, i.e. the maximum positive continuity in the direction from the tonic.
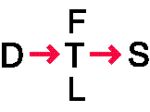
Phrygian function (F), is the grouping with the maximum impulse towards the tonic from above.
Lydian function (L), is the grouping with the maximum impulse towards the tonic from below, [10], [3].

2.3 Harmony and melody

We distinguish two classes of bindings with respect to their existence in time:

vertical bindings, i.e. interactions within one grouping (sounding at the same moment);
horizontal bindings, i.e. interactions between two successive groupings in the time. All things we can derive from the vertical bindings are part of harmonic statics, all other things belong to harmonic kinetics.

2.3.1 Harmonic statics

We inspect groupings isolated from any harmonic context in the harmonic statics.
The root is the tone having the zone with the maximum energy.

The entropy and genus of the grouping depend on the energy distribution among zones. The maximum entropy (dissonance) takes place when the energy of all tones is balanced.

Genus is a property of the best-ordered groupings. The positive genus corresponds to the grouping with a marked maximum, the negative genus to that with a marked minimum.

more on harmonic statics

2.3.2 Harmonic kinetics

The energy of a grouping depends on modality and its F-potentials in the harmonic kinetics. The distribution of the F-potentials in the tonality determines certain levels of particular groupings. The transition from one level to another results in a tension. (Tension and relaxation contrasts can also result from various amounts of entropy of the groupings, [10]).

Harmonic tendency (tendency of continuity and impulse) of chord (harmonic gradient) is determined by position of chord in tonality; it is not influenced by tension (entropy) inside of chord.

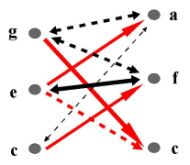
Harmonic connections act similarly, if particular bindings are equal or similar (as for quality and quantity). The measure of the link-up between groupings is the total value of the continuity or impulses in the bindings.

We distinguish direct harmonic stream (with the positive continuity to every following grouping) and reverse harmonic stream (with the negative continuity).

As music evolution goes on, the known groupings are enriched by new tones which were considered to be non-essential before, [2]. This results in an increased number of possible harmonic connections, but, on the other hand, the variety of possible extremely different levels of the F-potentials for groupings decreases, [1].

2.3.3 Melody

The energy remains in the zone until a tone in a next neighboring zone begins to sound.
A quick succession of mutually non-disturbing tones acts harmonically (e.g. tremolo), whereas the succession of interacting tones preserves its melodic character (e.g. trill).

Trill: (tones c-d disturb each other)
+ d + d + d ... c + c + c + c +

Tremolo: (tones c-e in resonant state)
+ e + e + e ... c + c + c + c +

We define harmonic power as total (time integrated) energy in zones. Hence harmonic power of melody with marked continuity is high (e.g. Alberti bass) whereas harmonic power of melody with marked impulse is low (e.g. a scale).
Harmonic skeleton of melody is a set of tones, which contribute mostly to the harmonic power.
more on harmonic kinetics

3.Implementation

3.1 Harmonic system

Regular 12-tone system, [8], is the most widespread system of the western music. It was, therefore, selected for the following description. Let us evaluate the bindings with the parameters of continuity and impulse. There is no exact way, how to derive precise values without knowing the substance of the interactions among the zones. The only source we know consists of the roots, [9], and various consonance amounts, [6], [9], of the selected chords. Also the values for the B-influences were derived using the known harmonic functions, [3], of some selected tonalities, see Table 1.

Interval characteristics

Table 1: Interval characteristics

Interval	-5	-4	-3	-2	-1	1	2	3	4	5	6
Continuity	-4	+2	0	0	0	0	0	0	-2	+4	0
Impulse	0	0	+1	+3	+12	+12	+3	+1	0	0	0
B-influence	+4	+2	-1	-1	-2	-2	-1	-1	+2	+4	0

Frame - continuity on horizontal axis, impulse on vertical axis.

The highest impulse

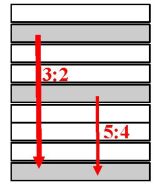
We suppose the highest impulse, I, is associated with the intervals of the semi-tone: I(1)=+12, whole tone: I(2)=+3, and minor third: I(3)=+1.
The action of impulses does not depend on the direction of the binding; it is therefore always positive.

The highest continuity

The highest continuity, C, is bound to the interval of the perfect fifth (resonance 3:2) and major third (5:4).
The continuity does depend on the acting direction.
The descending fifth has a positive continuity: C(-7)=C(+5)=+4; similarly, the descending major third: C(-4)=C(+8)=+2.

We neglect the impulses and continuities of other intervals.
Maximum impulse as well as maximum continuity tend to identity.

3.2 Tonality

We shall derive the values of some more general characteristics using the values defined in the preceding paragraphs.
Let us consider the bindings in the natural modality (c, d, e, f, g, a, b) first, and find out the interval with highest continuity, see Table 2.

Table 2: Intervals in natural modality

-	c	d	e	f	g	a	b
c	0	+2	+4	+5	-5	-3	-1
d	-2	0	+2	+3	+5	-5	-3
e	-4	-2	0	+1	+3	+5	-5
f	-5	-3	-1	0	+2	+4	+6
g	+5	-5	-3	-2	0	+2	+4
a	+3	+5	-5	-4	-2	0	+2
b	+1	+3	+5	+6	-4	-2	0

We see e.g. one fifth and one major third for the tone f, i.e. fc and fa, see Table 3.

Table 3: Intervals of continuity

-	c	d	e	f	g	a	b
Fifths	2	2	2	1	2	2	1
Major thirds	1	0	1	1	1	1	1

The tones c, e, g, a have the strongest continuity with other tones (two fifths and one major third). We suppose the tonic in the natural tonality is well ordered grouping consisting of these tones. We know two such groupings from the musical experience:

c,e,g is the tonic of the major key,
a,c,e is the tonic of the Aeolian minor key, [5].

The whole tetrad c,e,g,a is also found as the tonic in newer music.

Formal potential

We express numerically the F-potentials
of the zones derived from the B-influences
(the F-potential in the last column of Table 4
is the sum of the B-influences in the row):

Table 4: Influences of the zones

-	c	d	e	f	g	a	b	∑
c	0	-1	+2	+4	+4	-1	-2	+6
d	-1	0	-1	-1	+4	+4	-1	+4
e	+2	-1	0	-2	-1	+4	+4	+6
f	+4	-1	-2	0	-1	+2	-2	0
g	+4	-1	-1	-1	0	-1	+2	+7
a	-1	+4	+4	+2	-1	0	-1	+7
b	-2	-1	+4	-2	+2	-1	0	0

We see essentially the same results
we have derived in the above text,
i.e. the tones c, e, g, a have
the highest F-potential.
If we consider also secondary bands (bindings PS), we get values: g,a: 7; c,e:6; d:4; f,h:0; f#,a#:-2; g#, d#, c#:-4.

The following F-potentials, P, correspond to the selected groupings of the natural modality: P( C) = P(Ami) = 6.33; P( Emi) = P( F) = 4.33; P( Dmi) = P(G) = 3.67; P( Bmi5-) = 1.33. The values are determined for one tone, e.g. for C: P(C)=(c, e, g) = [P(c)+ P(e)+ P(g)]/3 = (6+6+7)/3 = 6.33.
more on musical potentials

Continuity towards the tonic

Similarly, the values of the continuity towards the tonic will be evaluated; this time the continuities of the bindings will be summed up, see Table 5. Note the extreme values for the dominants (+1.56) and subdominants (-1.56) towards both tonics.

Table 5: Continuity toward the tonics

Dmi	Emi	F	G	Bmi5-	to
-0.44	+1.33	-1.56	+1.56	+0.67	C
-1.56	+1.56	-1.33	+0.44	-0.67	Ami

Selected harmonic connections

We enumerate the values of continuity and impulse for some selected connections now, see Table 6.

Table 6: Some selected connections

Harmonic connection	Continuity	Impulse
EmiAmi, GC, CF	+1.56	2.11
EmiC, AmiF	+1.33	1.56
EmiF	+1.11	3.67
Bmi5-Emi, FBmi5-	+1.11	2.11
DmiG	+0.89	1.22
CAmi, FDmi	+0.89	0.56
Bmi5-C, AmiBmi5-	+0.67	3.67
GAmi, CDmi	+0.44	2.78
DmiEmi, FG	0.00	2.78
AmiAmi, CC	0.00	0.22
AmiEmi, CG, FC	-1.56	2.11

3.3 Harmony and melody

3.3.1 Harmonic statics

Let us investigate the bindings of continuity in the major, minor and augmented triads, [6].

Major and minor triad

The E column contains the resulting energy for the continuity in our example, see Table 7:

Table 7: Major and minor triads

-	c	e	g	E	-	a	c	e	E
g	-4	0	0	-4	e	-4	-2	0	-6
e	-2	0	0	-2	c	0	0	2	+2
c	0	2	4	+6	a	0	0	4	+4

The major and minor triads have the root c, [9], it is a bit more marked in the major one (E=+6) than in the minor one (E=+4). The entropy of both formations is about the same, the contradiction follows from their genus. The extreme value of the energy for the major triad is positive (E=+6), whereas the one for the minor triad is negative (E=-6).

Augmented triad

One of the (other) disputed issues is the imperfection of the consonance of the augmented triad ceg#, [6], see Table 8.

-	c	e	g#	E
g#	0	+2	-2	0
e	-2	0	+2	0
c	+2	-2	0	0

The energy of this triad is balanced. The higher entropy could be the cause of its imperfect consonance.

3.3.2 Harmonic kinetics

We could determine the modality at every time moment of musical stream precisely. This is especially difficult in the single-voice (una voce) songs. If there are only the tones: “c, d, e, f, g” in a song, we can not say in advance they are from the modality [c, d, e, f, g, a, b]. They could as well be e.g. from the modality [c, c#, d, e, f, g, g#] having quite different relations. Fixed modalities and groupings are idealizations. These structures are usually created dynamically by polyphony.
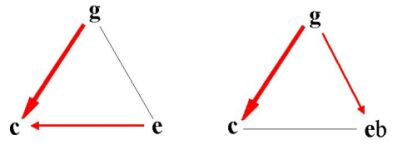
If the cadence e.g. in C major contains the sequence Db: G: C, so called Neapolitan sixth, [5], instead of the sequence Dmi: G: C, we cannot say we are still in the C major key.
Tones outside the modality are tolerated especially if their energy quickly vanishes due to the reactivity of the zones. This is the case of the chord Db; the energy in c#, g# zones are quickly neutralized when the dominant's tones d, g come.

3.3.3 Melody

Beginning of the Mozart's Alla-Turca March has simple harmonic skeleton - minor triad a,c,e. All other tones (g#,b,d,f) are in this context ornaments with melodic character only.

4. Application of the model

Musical styles

Every musical composition style has firm boundaries for the values of certain characteristics. The connections breaking the boundaries are considered not usual or they are literally prohibited by the rules of the style [7]. The limitations need not be applied to the whole harmonic connection only, but also to all its subjects, e.g. the prohibition of parallel fifths and octaves in the classical harmony. Some of the rules force partial phenomena to submit to the whole, e.g. the rules for the strict progression of the parts in the classical harmony permit such movement only that the sum of differences in the levels of all parts be minimal.

Some musical styles have their marked harmonic progressions. Let us name two of them. We find the following succession in the baroque music very often, [2], e.g. C: F: Bmi5-: Emi: Ami: Dmi: G: C. Let us evaluate the continuities between these consonant triad, see Table 6. We find practically the maximum positive values (1.56, 1.11, 0.89) in all partial connections.
The second typical progression can be found in jazz sequences, [11]. A normal jazz sequence (e.g. Ami7: D7: Gmi7: C7) resembles the baroque one as to the succession of the continuity. The chromatic jazz sequence (e.g. E7: D7: C7: B7) has, on the contrary, the extreme impulse of all partial connections.

4.2 Algorithmic composition

In this paragraph we shall outline the algorithm of generation of the tonal music harmonic stream.

We select the system order. We fill the matrices of the interval characteristics with the help of the empiric expressions.
We choose the modality.
We set the boundaries for possible groupings and generate the harmonic variety. Then we calculate the entropy, genus and F-potential of each grouping.
We plan the harmonic progression, i.e. the progression of the characteristics of particular connections.
We periodically search for the groupings satisfying the selected harmonic progression and keep record of the history of each harmony.

Conclusion

The theory of harmonic bindings was presented at the invited session "Fuzzy principles in music" of the Seventh IFSA World Congress, Prague, June 25-29, 1997 (International Fuzzy Systems Association).
The text presented here covers and extends the one printed in the conference proceedings.
Brief abstract was published in Proceedings of the International Seminar Mathematics and Music, Bratislava, 1997

I studied papers needed for developing of this theory during the years 1985-1988, the fundamentals of the theory arised in 1989.

Bibliography

[1.] Faltin Peter: Funkcia zvuku v hudobnej štruktúre (Sound Function in the Music Structure; in Slovak), Bratislava 1966.

[2.] Filip Miroslav: Vývinove zakonitosti klasickej harmónie (Evolutional Laws in the Classical Harmony; in Slovak), Bratislava 1965

[3.] Hradecký Emil: Úvod do studia tonální harmonie (Introduction to the Study of Tonal Harmony; in Czech), Prague 1972.

[4.] Janáček Leoš:Úplná nauka o harmonii (Complete Theory of Harmony; in Czech), Brno 1920.

[5.] Janeček Karel:Skladatelská práce v oblasti klasické harmonie (Practical Musical Composition in the Classical Harmony; in Czech), Prague 1973.

[6.] Janeček Karel:Základy moderní harmonie (Fundamentals of Modern Harmony; in Czech), Prague 1965.

[7.] Ludvová Jitka: Matematické metody v hudební analyze (Mathematical Methods in the Musical Analysis; in Czech), Prague 1975.

[8.] Risinger Karel: Intervalový mikrokosmos (Microcosmos of Intervals; in Czech), Prague 1971.

[9.] Risinger Karel: Hierarchie hudebních celků (Hierarchy of Musical Units; in Czech), Prague 1969.

[10.] Sín Otakar: Úplná nauka o harmonii na základě melodie a rytmu (Complete Theory of Harmony based on Melody and Rythm; in Czech), Prague 1943.

[11.] Velebný Karel: Jazzová praktika 1 (Jazz Practical Courses 1; in Czech), Prague 1983

[12.] Volek Jaroslav: Novodobé harmonic systemy (Modern Harmonic Systems; in Czech), Prague 1961

[13.] Volek Jaroslav: Struktura a osobnosti hudby (Structure and Personalities of the Music; in Czech), Prague 1988

-	c	d	e	f	g	a	b
c	0	+2	+4	+5	-5	-3	-1
d	-2	0	+2	+3	+5	-5	-3
e	-4	-2	0	+1	+3	+5	-5
f	-5	-3	-1	0	+2	+4	+6
g	+5	-5	-3	-2	0	+2	+4
a	+3	+5	-5	-4	-2	0	+2
b	+1	+3	+5	+6	-4	-2	0

-	c	d	e	f	g	a	b	∑
c	0	-1	+2	+4	+4	-1	-2	+6
d	-1	0	-1	-1	+4	+4	-1	+4
e	+2	-1	0	-2	-1	+4	+4	+6
f	+4	-1	-2	0	-1	+2	-2	0
g	+4	-1	-1	-1	0	-1	+2	+7
a	-1	+4	+4	+2	-1	0	-1	+7
b	-2	-1	+4	-2	+2	-1	0	0

-	c	d	e	f	g	a	b
c	0	+2	+4	+5	-5	-3	-1
d	-2	0	+2	+3	+5	-5	-3
e	-4	-2	0	+1	+3	+5	-5
f	-5	-3	-1	0	+2	+4	+6
g	+5	-5	-3	-2	0	+2	+4
a	+3	+5	-5	-4	-2	0	+2
b	+1	+3	+5	+6	-4	-2	0

-	c	d	e	f	g	a	b	∑
c	0	-1	+2	+4	+4	-1	-2	+6
d	-1	0	-1	-1	+4	+4	-1	+4
e	+2	-1	0	-2	-1	+4	+4	+6
f	+4	-1	-2	0	-1	+2	-2	0
g	+4	-1	-1	-1	0	-1	+2	+7
a	-1	+4	+4	+2	-1	0	-1	+7
b	-2	-1	+4	-2	+2	-1	0	0

-	c	d	e	f	g	a	b
c	0	+2	+4	+5	-5	-3	-1
d	-2	0	+2	+3	+5	-5	-3
e	-4	-2	0	+1	+3	+5	-5
f	-5	-3	-1	0	+2	+4	+6
g	+5	-5	-3	-2	0	+2	+4
a	+3	+5	-5	-4	-2	0	+2
b	+1	+3	+5	+6	-4	-2	0

-	c	d	e	f	g	a	b	∑
c	0	-1	+2	+4	+4	-1	-2	+6
d	-1	0	-1	-1	+4	+4	-1	+4
e	+2	-1	0	-2	-1	+4	+4	+6
f	+4	-1	-2	0	-1	+2	-2	0
g	+4	-1	-1	-1	0	-1	+2	+7
a	-1	+4	+4	+2	-1	0	-1	+7
b	-2	-1	+4	-2	+2	-1	0	0